Blog & White

Le flou

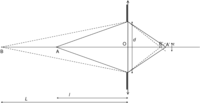
Lorsque la mise au point d'un système optique (simplifié) a été effectuée, l'image d'un objet ponctuel A situé à une distance l de l'objectif est un point A'. La mise au point est cependant imparfaite pour un objet B situé à une distance L plus (ou moins) loin que l : les rayons lumineux convergent en B' au lieu de A', continuent leur course et vont s'étaler autour de A' dans une zone de largeur ε. Sur le capteur d'un appareil photo, l'image B' de B est donc une tache circulaire dont le diamètre ε dépend de L, de la distance de mise au point l, de la distance focale f de la lentille et du diamètre d de la pupille, c'est-à-dire le trou circulaire par lequel la lumière entre dans la lentille, délimitée par le diaphragme. On considère ici que la pupille est suffisamment grande pour négliger les effets dûs à la diffraction.

On considère que l'image d'un point est net lorsque l'observateur (humain, en général) est incapable de faire la différence entre un « vrai » point et une tache. Le diamètre ε maximal d'une telle tache est lié au pouvoir de séparation de l'½il de l'observateur, qui est lié non seulement à la taille de la tache mais aussi à la distance à laquelle se situe l'observateur : plus l'observateur est éloigné, plus il est difficile de distinguer une petite tache d'un « vrai » point. La valeur de cet ε maximal n'est pas universelle, car elle dépend in fine de l'affichage de la photo (sur écran ou en tirage papier) et de la manière dont on regarde cette photo : il sera par exemple plus facile de remarquer un flou en regardant de près une image tirée en grand format qu'en regardant de loin une image tirée en petit format.

La profondeur de champ

D'après l'article de Wikipedia sur la Profondeur de champ, les limites de distance où les objets donneront une image considérée comme nette, une fois choisie un valeur ε maximale sont

L = l / (1 ± εl/df)

Les objets dont la distance est située entre ces limites auront une image considérée comme nette, car la tache de diamètre ε est trop petite pour être distinguée d'un « vrai » point net. On remarque que pour photographier un objet donné situé à une distance l en utilisant un objectif de distance focale f donnée, ces deux valeurs limites ne dépendent que du diamètre de la pupille, et pas du tout de la taille du capteur de l'appareil photo. Plus précisément, si les pixels du capteur sont plus grands que ε il n'y aura aucun flou car la tache circulaire sera contenue dans un seul pixel. Si les pixels sont plus petits que ε mais que les pixels à l'affichage de la photo (sur écran ou sur papier) sont plus grands que la tache circulaire, alors il n'y aura aucun flou à l'affichage, mais on pourra voir le flou en zoomant dans l'image (ce qui revient à dire que les pixels d'affichage deviennent plus petits que la tache circulaire).

Le nombre d'ouverture et la focale équivalente

La taille d de la pupille est exprimée dans la pratique non pas en millimètres, mais en fraction 1/N de la distance focale de l'objectif : d = f / N. N est le nombre d'ouverture et vaut donc N = f / d.

Si considère qu'en utilisant un objectif de distance focale f sur un capteur de taille différente on a une distance focale équivalente f_eq = kf, alors on peut écrire

N = feq / kd

où k est appelé « crop factor », soit

kN = feq / d

En introduisant la notion de nombre d'ouverture équivalent N_eq défini par N_eq = kN, la formule précédente devient

Neq = feq / d

qui est a la même forme que la définition du nombre d'ouverture, mais en utilisant le nombre d'ouverture équivalent et la focale équivalente.

Hyperfocale

On peut définir F = df/ε. En remplaçant le diamètre de la pupille d par son expression utilisant la distance focale et le nombre d'ouverture, on obtient

F = f2/εN

Les distances limites de la profondeur de champ deviennent alors

L = lF / (F ± l)

La distance hyperfocale F est la distance l minimale pour laquelle tous les objets entre F/2 et l'infini sont nets. Un corrolaire est que lors d'une mise au point à l'infini, tous les objets situés au delà d'une distance F sont nets.

Si on utilise la distance hyperfocale comme unité de distance de mise au point photographié, on peut représenter, de manière générique pour n'importe quelle combinaison de capteur, distance focale et nombre d'ouverture, les distances limites entre lesquelles les objets forment des images nettes (en supposant toujours que la distance focale est négligeable par rapport à la distance de mise au point).

En notant l = qF, on peut exprimer L en fonction de q et F:

L = qF / (1 ± q)

Le diagramme ci-contre indique les limites minimum et maximum de netteté pour une mise au point égale à une fraction de la distance hyperfocale F. On remarque que vers 0,9F, la limite maximum de netteté est déjà à 10F, et tend vers l'infini lorsqu'on se rapproche de 1F. Si on fait la mise au point à une valeur supérieure à F, la limite maximum de netteté reste à l'infini alors que la limite minimale n'augmente comparativement que très peu.

Le diagramme ci-contre représente les limites de netteté pour des distances de mise au point inférieures à 0,5F. On remarque que lors d'une mise au point à 0,5F, les objets situés au delà de F ne sont plus nets.