Mardi, 31 décembre 2019
Catégories : [ Livres/BD/Largo Winch ]

© Amazon.fr
Largo rencontre un criminel russe qui lui apprend que le groupe W est coté sur
un marché souterrain et qu'il a machiné la perte de valeur du groupe W afin de
gagner de l'argent sur ce marché là, où il avait parié sur la baisse de la
cotation du groupe W. Aidé d'une agent du FSB infiltrée chez le criminel,
Largo s'enfuit et trouve refuge chez un homme d'affaires Russe avent de
rentrer aux États-Unis et de refiscaliser son groupe. Un peu plus tard, il
apprend que l'homme d'affaires Russe est à l'origine du complot, car ce
dernier avait parié sur la hausse de la cotation du groupe W sur le marché
souterrain et voulait d'abord faire baisser la cotation autant que possible.
[ Posté le 31 décembre 2019 à 01:10 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Largo_Winch/les_voiles_ecarlates.trackback
Commentaires
Aucun commentaire
Lundi, 30 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Livres/BD/Golden City ]

© Amazon.fr
Harrison est élu maire de Golden City. Lors de la fête, Solo est tué par une
bande de gosses de riches qui voulaient s'amuser avec un pauvre. Ses amis
enquêtent pour trouver ce qui lui est arrivé. En parallèle, les opposants
politiques de Harrison révèlent à la presse que l'une de ses entreprises en
Russie fait du trafic d'organes volés sur des cadavres. Harrison se rend sur
place, se frotte à la mafia locale qui le fait mettre en prison lorsqu'il
refuse de continuer le trafic. Lorsque le criminel torture Amber, Il fait mine
d'accepter sa proposition, mais le fait assassiner sitôt rentré à Golden City.
[ Posté le 30 décembre 2019 à 19:23 |
1
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Golden_City/amber.trackback
Commentaires
Dark Web
Commentaire N° 1, Blog & White
le 4 janvier 2022 à 19:58
Catégories : [ Livres/BD/Troy ]

© Amazon.fr
Pour sauver le village troll d'une boule de feu tombant du ciel, Waha arrête
le temps dans tout le village. Elle part alors à la recherche d'un dragon de
neige pour éteindre le feu avant de laisser le temps reprendre son cours. Elle
trouve un dragon dans une station de sports d'hiver, mais ce dernier est lié
par contrat à la station et ne peut la quitter. Waha parvient à détruire le
contrat, à faire venir le dragon au village et à sauver les trolls.
[ Posté le 30 décembre 2019 à 19:14 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Troy/un_caillou_sur_la_tete.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Yoko Tsuno ]

© Amazon.fr
Dans une première partie, Yoko, Emilie et Bonnie repartent en 1935 pour sauver
deux enfants d'un accident sur un passage à niveau. Dans une deuxième partie,
Yoko et Emilia doivent convoyer par avion deux momies égyptiennes qu'un lord
Anglais veut renvoyer en Égypte. Emilia apprend de Dinah, la pupille du lord,
que la deuxième momie est en fait le corps de l'épouse du lord que ce dernier
a tuée et embaumée trois ans plus tôt avec l'aide forcée de Dinah. Lors du
vol, elles découvrent à bord de l'avion une bombe dont elles se débarrassent
et de preuves que le lord est un espion travaillant pour les Chinois. Ayant
fait demi-tour, elles sont attaqués à l'atterrissage par le lord qui y perd la
vie.
[ Posté le 30 décembre 2019 à 19:08 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Yoko_Tsuno/anges_et_faucons.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Livres/BD/Blake et Mortimer ]

© Amazon.fr
Arrivé à Hong Kong, Blake part à la recherche de Mortimer. Pendant ce temps,
ce dernier est transporté par ses ravisseurs vers leur camp en Chine
continentale. Il apprend que le chef de ces derniers veut utiliser le texte
caché dans un objet historique volé pour le légitimer comme dernier
descendant d'un empereur du passé qui aurait obtenu la vie éternelle mais
aurait disparu après avoir refusé d'em payer le prix. Durant sa captivité,
Mortimer retrouve Nasir, très malade, et pour le soigner s'enfuit avec la
complicité d'un malfrat qui veut un trésor mentionné dans la légende de
l'empereur. Après un périple ils trouvent l'empereur, toujours en vie, et
Mortimer parvient à trouver le remède magique pour Nasir. Il est recueilli par
hasard par Blake, parvient à guerir Nasir, puis tous s'enfuient à bord de
l'Aile Rouge que le chef des criminels avait récupérée et que Mortimer était
censé réparer lors de sa captivité. Pendant ce temps, Olrik vole le prototype
secret Britannique, mais échappe à sa destruction par les autorités.
[ Posté le 30 décembre 2019 à 18:35 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Blake_et_Mortimer/la_vallee_des_immportels_2.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Asterix ]

© Amazon.fr
Deux Arvernes confient Adrénaline, la fille de Vercingétorix, au village
Gaulois pour la protéger des Romains qui veulent la capturer. Adrénaline, qui
refuse de continuer à servir aux Gaulois et aux Romains de prétexte pour se
faire la guerre, s'enfuit sur le navire des pirates. Le navire est attaqué
d'abord par un renégat Gaulois au service des Romains, puis par les Romains
eux-mêmes. Elle finit par partir sur le navire d'un jeune Breton, affrété par
les Arvernes, et qui devait à l'origine la mettre à l'abri en Bretagne.
[ Posté le 30 décembre 2019 à 18:19 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Asterix/la_fille_de_vercingetorix.trackback
Commentaires
Aucun commentaire
Dimanche, 22 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
One night, Kevin is woken up in his room by a knight in armor coming out of
his cupboard, who soon disappears without a trace. The next night, ready with
a Polaroid camera, a band of dwarves appear and take him with them to the time
of Napoléon's Italian campaign. They manage to loot Napoléon's treasure and
use a map they have stolen from the Supreme Being to escape to the time of
Robin Hood (who takes all their loot to give to the poor). Meanwhile, the Evil
One is influencing the dwarves in order to attract them to his castle and
steal the map. Escaping from Robin Hood's time, Kevin is sent to Mycenaean
Greece where he meets Agamemnon, who takes him as an adoptive son. The dwarves
reappear as a group of entertainers, steal some treasure and take the boy with
them aboard the Titanic. After the ship has sunk, Evil transports the group to
his Time of Legends, where they are rescued by the ship of an ogre. They
escape the giant who carries the ship as his hat, and finally arrive at the
Fortress of Ultimate Darkness, where Evil takes the map and locks them up in a
cage hanging above a bottomless pit. The group manages to escape by swinging
from the cage to the edge of the pit, finds Evil's headquarters, steal the map
and split. The dwarves go away using the map while Kevin attempts to distract
Evil, until the band comes back from various time periods with weapons and
warriors. They prove unsuccessful and all seems lost when Evil suddenly bursts
into flames. The Supreme Being appears and explains he had influenced the
dwarves into stealing the map so that they would test the abilities of Evil
(yet another creation of the Supreme Being). The dwarves collect the ashes of
Evil, and then leave with the Supreme Being, leaving Kevin alone. Kevin then
wakes up in his bed, the house on fire, and is taken out by a fireman. His
parents then discover one smouldering remain of Evil, touch it and disappear.
The whole world then gets rolled up into the map.
[ Posté le 22 décembre 2019 à 23:30 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/time_bandits.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Samuel Smith ]

Nice stout, quite sweet. Contains barley and oatmeal.
Samuel Smith, Tadcaster, North Yorkshire, England. 5% alcohol
[ Posté le 22 décembre 2019 à 23:07 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Samuel_Smith/samuel_smith_s_oatmeal_stout.trackback
Commentaires
Aucun commentaire
Lundi, 16 décembre 2019
Catégories : [ TV/Cinéma/Tati ]

Wikipedia
Monsieur Hulot passe ses vacances à la mer. Il parle peu, se montre maladroit
et commet bourde sur bourde (il repeint un canot qui se casse en deux et
ressemble à là gueule d'un monstre marin ; il crève un pneu de son tacot sur
le chemin d'un pique-nique et se retrouve dans un cimetière durant un
enterrement ; il se perd la nuit dans une cabane remplie de feux d'artifices
et les fait tous brûler). À la fin des vacances tout le monde quitte l'hôtel ;
il ne s'est rien passé de notable.
[ Posté le 16 décembre 2019 à 21:02 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/Tati/les_vacances_de_monsieur_hulot.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Samuel Smith ]

“palate of beech nuts, almonds and walnuts”
Maybe a bit nutty, but just another ale. Contains malted barley.
Samuel Smith, Tadcaster, North Yorkshire, England. 5% alcohol
[ Posté le 16 décembre 2019 à 20:06 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Samuel_Smith/samuel_smith_s_nut_brown_ale.trackback
Commentaires
Aucun commentaire
Samedi, 14 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Science ]
I have over forty Ni-MH low self-discharge rechargeable batteries (mostly
Eneloops, and a few Vartas and GPs) and I have noticed that some of them tend
to not keep the charge very well. In order to find out which ones are worth
throwing away to be recycled, I needed a device that would measure their
capacity.
The principle is very simple: recharge the battery, discharge it through a
resistor with a known value, measure the current while it discharges, and
integrate the current over time. This will give you the battery's capacity.
A few things need to be taken into account: how do you know that a battery is
depleted and what discharge current should be used? From what I could gather
by reading a few Web forums, the battery is considered to be depleted when its
voltage goes below 1.0 V or 0.9 V (I settled on 1.0 V), and the current should
be such that the battery discharges in about five hours (for a 2000 mAh battery,
that would be about 400 mA). If the current is too high, the battery's voltage
while it is discharging will be very close to 1.0 V already at the beginning
of the process and the capacity measurement will probably be biased. I noticed
this in the first iteration of the device where I had a 1 Ω resistor and
a 1 A current, and decided to change for a 3.3 Ω resistor after reading
about the “discharge in 5 hours” rule.
The device

The prototype I built is very simple. The battery discharges through a
3.3 Ω ±1% 0.6 W resistor, and the voltage is measured using the
Arduino's ADC (more on that below). A MOSFET (STMicroelectronics VNP35NV04-E,
quite expensive but it turns fully On with only 2.5 VGS and its On
resistance is only 13 mΩ, which is below the tolerance of the main
resistor and the accuracy of what the Arduino can measure, so it can simply be
ignored) controls the discharge and cuts the current once the “depleted”
threshold has been reached to prevent damaging the battery. A 10 kΩ
resistor acts as a pull-down for the MOSFET's gate, and a 110 Ω limits
the gate current (whether it's really needed or not seems to depend whom you
ask on Web forums, but since I had some lying around I decided to use them).
There are two instances of the circuit on the prototype board, so I can test
two batteries in parallel.
Accuracy of the Arduino's ADC
The Arduino's ADC has a maximum precision of 10 bits, meaning that the value
read from e.g., A0 is translated to a value between 0 and 1023 included, by
comparing A0 to a reference voltage that by default is the Arduino's supply
voltage. It is however possible to get (reasonably) accurate voltage
measurement with the Arduino (see this Web post titled
Secret Arduino Voltmeter)
by measuring first the supply voltage accurately against the ATMega328's internal
band-gap reference. To do so, you need to first measure the band-gap
reference's correct value (it's about 1.1 V, it's very stable over time and
temperature, but it's exact value differs from one ATMega328 to the next).
The process therefore goes like this.
- With a trusted voltmeter, measure the Arduino's supply voltage
VCC as accurately as possible.
- Using the code snippet in the blog post, measure the band-gap's value
with the ADC; that gives you a number Nref. For better accuracy,
compute the arithmetic mean of 1000 measurements to get rid of the random
fluctuations in the measurement.
- Calculate Vref = Nref × Vcc / 1024 (and not
1023 as stated in the blog post). In my case,
Vref = 1.089 V ±0.001V.
- Hardcode the Vref you have found in your Arduino program.
Then when you want to actually measure a voltage V with the Arduino's ADC, do
as follows.
- Measure Nref with the ADC and compute the value of
Vcc = Vref × 1024 / Nref (again, take the
average of 1000 measurements).
- Measure N with the ADC and compute the value V = N × Vcc / 1024
(once again, average over 1000 measurements).
If my uncertainty calculations are correct, I get a 0.12% uncertainty on the
value of Vcc (compounding the uncertainty of the voltmeter and the
ADC), which is less than the 1% uncertainty on the discharge resistor value. I
tried to accurately measure the 3.3 Ω resistor value, but my amperemeter
is not accurate enough for currents above 200 mA, so that's the best I can
hope to achieve.
Take a look at the code
if you want to know the details of the implementation (especially computing in
millivolts in order to use only integers instead of floats).
What about those batteries, then?
I measured the capacity of 27 batteries so far: 2 GPs, 3 Vartas and
22 Eneloops (6 of generation 1, 7 of generation 2, 2 of generation 3 and 7 of
generation 4). All have a nominal capacity of 1900 mAh.
Both GPs have a capacity of 1 mAh, so they are useful only as paperweights.
The Vartas have capacities of 870, 450 and 250 mAh, so they are only
marginally more useful than the GPs.
One Eneloop is in really bad shape (200 mAh), but the others have capacities
between 1660 and 1900 mAh, with a mean of 1790 mAh.
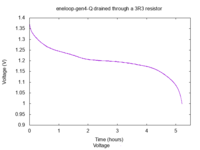
This is a typical battery, in good shape (1890 mAh). The voltage quickly drops
to around 1.2 V and remains stable for a while before dropping again.
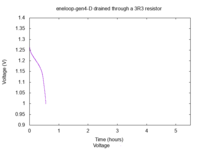
This one is definitely good for nothing (200 mAh). I remember accidentally
dropping batteries on the floor a couple of times in the past, maybe this one
suffered from it?
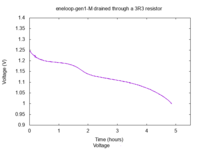
This one is a first generation eneloop, bought probably around 2011. It still
has a capacity of 1660 mAh, but the shape of the curve is different from the
typical one, maybe due to old age?
[ Posté le 14 décembre 2019 à 17:08 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/battery_capacity_meter.trackback
Commentaires
Aucun commentaire
Jeudi, 12 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Sara and Beethoven spend the summer at Sara's uncle Freddy in a small town
called Quicksilver. During at stroll in the mountain, Beethoven returns with
an old 10 dollar bill which is quickly identified as part of the treasure
hidden by a bank robber couple in the 1920s, and is worth a lot more to
collectors. Soon many inhabitants go searching for the loot, while Sara gets
repeatedly threatened by someone who obviously doesn't want her to find the
treasure. Searching for information about the robbers, Sara and her friend
Garrett start by suspecting the grumpy librarian, but they eventually manage
to get Beethoven to lead them to the treasure (in the old mine) where they are
attacked by the head of the local chamber of commerce; the librarian is
innocent even if he's the direct descendant of the robbers.
[ Posté le 12 décembre 2019 à 22:42 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/beethoven_5.trackback
Commentaires
Aucun commentaire
Lundi, 9 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Abby's career in astrophysics comes to an abrupt end when her dean discovers
she had she appears in a video with her friend Erin (who does scientific
research on paranormal phenomena in a lesser university and gets kicked out as
well) documenting an authentic apparition in an old New York manor. With the
help of Erin's lab engineer Jillian, they decide to do proper scientific
research on the topic, setting up their laboratory above a Chinese restaurant.
They are called by Patty, an MTA employee who also witnesses an apparition in the
metro, and discover that the ghost has been “called” by an electronic
device. Jillian develops gadgets capable to grab a ghost and eventually trap
it. They get into trouble when a debunker gets killed by the ghost he released
from the trap, and are told by the mayor that supernatural activity is usual
in New York, under the jurisdiction of the DHS, and that they must keep it
quiet. The team eventually discovers that a man called Rowan is planting the
devices is specific locations to eventually cause a paranormal catastrophe.
They locate the main device in the basement of a hotel, but cannot prevent
Rowan from dying of electrocution. Rowan killed himself on purpose, to take
control of the army of ghosts that he releases. While the police and DHS
agents are subdued by the ghosts, the Ghostbusters manage to go through and
throw their car and its nuclear generator into the vortex coming out of
Rowan's device, effectively closing it.
[ Posté le 9 décembre 2019 à 20:43 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/ghostbusters_2016.trackback
Commentaires
Aucun commentaire
Dimanche, 8 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Belhaven ]

“Scottish triple malts… chocolate malts… fresh roasted aroma… hint of
coffee… dark chocolate complexity… hopped with Challenger”
Roasted yes, chocolate not really. Contains oats and malted barley.
Belhaven Brewery Company Ltd., Dunbar, Scotland. 4.2% alcohol.
[ Posté le 8 décembre 2019 à 11:57 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Belhaven/belhaven_blackt.trackback
Commentaires
Aucun commentaire
Mardi, 3 décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Beethoven meets a female St. Bernard named Missy, just before she is kidnapped
by Regina, the ex-wife of her owner who wants to pressure her ex-husband for
money. Beethoven manages to find Missy and they have puppies together, before
Missy is taken again. The Newton children find and raise the puppies in the
absence of their mother, at first hiding them from their grumpy father. Then
the whole family and the dogs go away in the mountains for the 4th of July.
There Beethoven finds Missy again (her kidnapper happens to spend her vacation
in the same place as the Newtons) and escapes with her into the mountain. Regina
steals the puppies from the Newtons and then goes after the two escaped
dogs. She is followed by the Newtons who eventually catch up with her, defeat
her and recover the puppies with Beethoven's help.
[ Posté le 3 décembre 2019 à 22:49 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/beethoven_2.trackback
Commentaires
Aucun commentaire
Dimanche, 1er décembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Little Valley ]

“smokey flavours and hints of moorland heather”
Not distinctly smokey, a bit sweet, not bad. Contains malted barley, malted
wheat, peat malted barley.
Little Valley Brewery, Hebden Bridge, West Yorkshire, England. 5.5% alcohol.
[ Posté le 1er décembre 2019 à 21:24 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Little_Valley/little_valley_moor_ale.trackback
Commentaires
Aucun commentaire
Mardi, 26 novembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
While kidnapping puppies for an evil scientist who uses dogs as test animals,
a St. Bernard puppy escapes and is adopted by the Newton family, despite the
opposition of the grumpy father. The children name him Beethoven, and he
starts by ruining the house on a regular basis. While growing up, Beethoven
also helps the family in various ways. On a trip to the veterinarian, the
latter (who is the evil scientist from the beginning) devises a scheme to take
the dog. He visits the family, simulates being attacked by Beethoven, and
convinces the father to get the dog put down. The family discovers that their
dog is not actually going to be euthanized, and follow the veterinarian to his
lair, where Beethoven has managed to escape and causes chaos among the
villains. Having been alerted, the police arrives and arrests the culprits,
and the Newton adopt all the other dogs that were prisoner from the villains.
[ Posté le 26 novembre 2019 à 22:39 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/beethoven.trackback
Commentaires
Aucun commentaire
Lundi, 25 novembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bière ]

“tropical fruit… hop bitterness”
Just another beer, quite good. Contains malted barley and wheat.
The Ilkley Brewery co., Ilkley, West Yorkshire, England. 5.5% alcohol.
[ Posté le 25 novembre 2019 à 22:35 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/ilkley_fruition.trackback
Commentaires
Aucun commentaire
Jeudi, 21 novembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bricolage ]
For quite a while I have been dreaming about a lamp for reading in bed that
would be equally usable when lying on my belly or sitting with my back on the
wall. It would be wide enough to uniformly light an open comic book (slightly
larger than an A3 paper sheet) without causing a glare on the paper, meaning
that it should light from above. Finally it must be made of a strip of warm
white LED, its brightness must be adjustable and must consume no power when
it's off.
And because making things is fun, I wanted to make it myself. There it is.

It's made of 60 cm of LED strip glued on the inside of a 15×15 mm
aluminium profile, and it's powered by a 12 V, 500 mA power supply, via a
dimmer (that has also silly features like strobe effect, blinking and
pulsating, but that's no good for reading). The power supply is connected to
the mains via a wire equipped with a switch (that effectively cuts the power
to the power supply when it's off).


To meet the requirement of reading in two different positions, the angle of
the aluminium profile can be changed by rocking it. I had to solder thinner
wires to the LED strip to prevent it from acting like a spring and holding the
lamp back when rocking it.


[ Posté le 21 novembre 2019 à 17:42 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Bricolage/bed_reading_lamp.trackback
Commentaires
Aucun commentaire
Dimanche, 10 novembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma/Monty Python ]

Wikipedia
Brian is born one stable away from Jesus. As an adult, he falls in love with
Judith, who is a member of the People's Front of Judea. Brian joins the rebel
organization, and after a failed attempt against Pontius Pilatus, he barely
escapes the clutches of the Roman leader. In an attempt to hide from the Roman
legionaries who chase him, he pretends to be one of the many prophets who
speak on the street, but for some reason he attracts an audience who follows
him everywhere. Brian is eventually captured by the Romans and sentenced to be
crucified. As is the tradition, Pilatus asks the crowd which one of the
condemned men should be released, and Brian's name is called. Alas, due to a
misunderstanding, another man is released, and all of Brian's friends
acknowledge that his martyr will be a great help to the People's cause, and
leave him to die.
[ Posté le 10 novembre 2019 à 22:46 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/Monty_Python/life_of_brian.trackback
Commentaires
Aucun commentaire
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

“kuusenkerkällä ja hunajalla maustettu Barley Wine”
Tuoksuu ruisleivältä, tosi makea ja maistuu vähän kuusenkerkältä. Sisältää
ohramallasta ja ruismallasta.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 10.5% alkoholia.
[ Posté le 10 novembre 2019 à 20:13 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_kouko.trackback
Commentaires
Aucun commentaire
Dimanche, 3 novembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Swannay ]

“American hops… British malt”
Very sweet, kind of fruity and not too strong. Quite good. Contains malted
barley and wheat.
Swannay Brewery, Orkney, Scotland. 8.0% alcohol.
[ Posté le 3 novembre 2019 à 11:36 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Swannay/swannay_old_norway.trackback
Commentaires
Aucun commentaire
Mercredi, 23 octobre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Robert Langdon wakes up in hospital in Florence and has lost his recent
memory. He is attacked by a killer dressed as a policewoman, and makes a
narrow escape with Sienna Brooks, the doctor who was treating him. In his
belongings he discovers a device that projects a representation of Dante's
Inferno, in which a message has been hidden. They discover that the
recently deceased billionaire Zobrist has created a viral weapon meant to
solve overpopulation by killing a large portion of the world's population.
Escaping agents of the WHO, they follow clues in Florence and Venice. They
are contacted by an agent of WHO who reveals himself to be a freelancer trying
to get the virus and resell it, and are saved by a man hired originally by
Zobrist who has changed allegiance when he discovered the billionaire's plan.
He reveals to Langdon that the amnesia has been medically induced and that the
whole story is a setup to put Langdon on the track of the virus after
Zobrist's death. Langdon finally finds a clue about the virus being in the
Hagia Sofia in Istanbul, after which Brooks, who reveals herself as Zobrist's
lover, decides to ensure it will be released. Langdon and the real WHO agents
finally locate the virus in a water reservoir and manage to contain it just
before it was due to be released.
[ Posté le 23 octobre 2019 à 22:57 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/inferno.trackback
Commentaires
Aucun commentaire
Mardi, 22 octobre 2019
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

Tosi makea ja väkevä, maistuu kahville ja paahtanelle. Sisälttäa ohramallasta.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 12.0% alkoholia.
[ Posté le 22 octobre 2019 à 22:43 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_ikiiurso.trackback
Commentaires
Aucun commentaire
Samedi, 19 octobre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
At CERN, a small container of anti-matter (yes, I know) is stolen while the
word mourns the death of the Pope. Soon after, Robert Langdon is asked by the
Vatican police to help in a case of kidnapping of the four cardinals who are
the favourites in the upcoming election of the next Pope. The kidnapper
promises to kill them at an hour interval between 8PM and 11PM, and that at
midnight the antimatter would explode and destroy the Vatican and most of
Rome. The clues indicate that he belongs to the Illuminati, a society of early
scientists persecuted by the Church for their teachings and who has gone
underground since then. In the meanwhile, the remaining cardinals start the
conclave to elect the new Pope. Langdon deduces that the kidnapped cardinals
will be killed at the location of a secret path of four steps (related to the
four elements) across Rome that leads to the Illuminati's secret meeting
place. They also find a proof that the Pope had been murdered. Langdon,
Vittoria (a physicist from CERN who worked on the antimatter) and the police
arrive too late to save the first victim, who is found under the Chigi chapel.
They also arrive too late to save the second cardinal, murdered on St. Peter's
Square, and the third one, burned alive in Santa Maria della Vittoria, where
the kidnapper kills most of the policemen accompanying Langdon. In the
meanwhile McKenna the Camerlengo fails to convince the cardinals to break the
conclave and to evacuate the Vatican. Langdon manages to save the fourth one,
Baggia, from being drowned in the Fontana dei Quattro Fiumi, who reveals they
were kept prisoner in the Castel Sant'Angelo. Langdon and Vittoria go there
with the police but get separated from them. The discover that McKenna is
meant to be the next victim and they return to the Vatican through an ancient
secret passage. They arrive just in time in the Pope's apartments to see
McKenna threatened by Richter, the chief of the Swiss guard, who get killed by
the police. Langdon then deduces that the antimatter is hidden in St. Peter's
tomb. As only a few minutes remain before midnight, McKenna, having been
trained in the Irish Air Force, takes the container and flies it up with a
helicopter before jumping with a parachute. The explosion happens in high
altitude, and the Vatican suffers only minor damage. The cardinals then
consider making McKenna the new Pope, despite the fact he's not a cardinal.
Just before dying Richter had given Langdon a key to access video recordings
of the Pope's apartments, where Langdon discovers that the kidnapping has been
organised by McKenna with the purpose of becoming the next Pope; the
Illuminati is only a convenient common enemy to unite the Church against the
perceived blasphemy of reconciling science and religion. Seeing no issue,
McKenna commits suicide and the conclave elects Baggia as the new Pope.
[ Posté le 19 octobre 2019 à 23:33 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/angels_and_demons.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Robert Langdon is suspected by the French police to have murdered the curator
of the Louvre, who has been found naked and surrounded with cryptic symbols.
Langdon deduces from them that the curator was a grand master of the Priory of
Sion, a secret society sworn to protect the Holy Grail. With the help of
Sophie, a police cryptographer who believes Landgon is innocent, and based on
the symbols, they find in the Louvre a key hidden by the curator and escape
the policemen. The key leads them to a bank where they retrieve a device
containing a hidden message and requires a password to open. To hide from the
police, they go to Sir Leigh Teabing, an expert on the Holy Grail. Teabing
convinces them that the Holy Grail is actually a woman, none other than Maria
Magdalena, Jesus' wife, and that the Priory of Sion has been protecting the
descendants of Jesus ever since. They are also chased by a religious fanatic
from Opus Dei who attempts to kill them (and who already killed the curator),
with the aim to destroy proof of the existence of Jesus' descendants. They
escape to London using Teabing's private jet, hoping to find the clue to
unlock the device. They are betrayed by Teabing's butler who works for Opus
Dei. They finally discover that Teabing is the one who was tipping the Opus
Dei with the purpose of bringing down the Catholic Church for centuries of
deceit regarding the truth about the Holy Grail. Threatened by Teabing, they
go to Westminster Abbey where Langdon finds the key to open the device and
eventually causes Teabing to be arrested by the police. The message in the
device indicates that the Holy Grail lies “beneath the Rose”, leading the
heroes to Rosslyn Chapel in Scotland, where they find the Priory of Sion's
archives and proof that Sophie is the last descendant of Jesus. But the
sarcophagus of Maria Magdalene is not there anymore, preventing any kind of
genetic test against Sophie's DNA. In the end, Langdon understands that the
rose is a reference to the “rose line” and that the sarcophagus is buried
below the Louvre's inverted pyramid.
[ Posté le 19 octobre 2019 à 22:52 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/the_da_vinci_code.trackback
Commentaires
Aucun commentaire
Dimanche, 6 octobre 2019
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

“vehnäolut… savu, kataja ja ruis”
Yllättävä katajanmarjan maku, myös vähän savuinen. Sisältää vehnämallasta,
ohramallasta ja katajanmarjaa.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 5.5% alkoholia.
[ Posté le 6 octobre 2019 à 14:34 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_kare.trackback
Commentaires
Aucun commentaire
Samedi, 5 octobre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma/Monty Python ]

Wikipedia
Lots of loosely related sketches, in front of a live audience.
[ Posté le 5 octobre 2019 à 22:47 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/Monty_Python/monty_python_live_at_the_hollywood_bowl.trackback
Commentaires
Aucun commentaire
Lundi, 30 septembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Science ]
Given a week number, it's not easy to know when it is located in the
calendar. And to add to the confusion, there are three definitions of the week
number (ISO-8601; Middle Eastern; North-American and Islamic). The EU and most
European countries use the ISO-8601 definition, according to
Wikipedia.
The following method is quite approximative so the actual definition does not
matter so much, but it should help placing a week number in the calendar
without having to look it up:
- Divide by 4
- Subtract 10%
- Add 1
The integer part (before the decimal separator) of the result is the number of
the month, and the fractional part (after the decimal separator) times three
tells you near what day of the month it is located.
For example:
- Week 1: 1/4 is 0.25, minus 10% is about 0.2, plus 1 is 1.2; 2 times 3 is 6:
it's around January 6th (Jan. 1-5, 2019 actually).
- Week 7: 7/4 is 1.75, minus 10% is about 1.6, plus 1 is 2.6; 6 times 3
is 18: it's around February 18th (Feb. 10-16, 2019 actually).
- Week 14: 14/4 is 3.5, minus 10% is about 3.2, plus 1 is 4.2; 2 times 3
is 6: it's around April 6th (Mar. 31-Apr. 6, 2019 actually).
- Week 42: 42/4 is 10.5, minus 10% is about 9.5, plus 1 is 10.5; 5 times
3 is 15: it's around October 15th (Oct. 13-19, 2019 actually).
- Week 35: 35/4 is 8.75, minus 10% is about 7.9, plus 1 is 8.9; 9
times 3 is 27: it's around August 27th (Aug. 25-31, 2019 actually).
- Week 52: 52/4 is 13, minus 10% is about 11.7, plus 1 is 12.7; 7 times 3
is 21: it's around December 21st (Dec. 22-28, 2019 actually).
[ Posté le 30 septembre 2019 à 18:13 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/week_numbers.trackback
Commentaires
Aucun commentaire
Catégories : [ Science ]
Suite à des discussion sur la distance focale équivalente d'un objectif monté
sur des appareil photo numériques équipés de capteurs de différentes tailles
et sur des notions exotiques comme l'ouverture équivalent et la sensibilité
équivalente évoquées par Richard Butler sur dpreview.com, je me suis penché
sur la question de la pertinence de ces concepts. Les articles suivants
publiés précédemment sur mon blog présentent les résultats de mes réflexions.
- L'angle de champ
- La profondeur de champ
- La perspective
- La sensibilité
- Le temps de pose
- L'affichage d'une photo
Je ne m'intéresse à la photo que sous l'angle de l'optique, et comme je ne
suis pas photographe pour deux sous, j'ai peut-être écrit des énormités ; si
c'est le cas, on peut poster des commentaires sous les articles et tenter de
me convaincre que je me suis trompé.
Caractériser une photo
Une photo est souvent caractérisée par le modèle d'appareil ayant servi, ainsi
que par la distance focale de l'objectif utilisé, le nombre d'ouverture et le
temps de pose. Étant donné la confusion créée par la notion de distance focale
équivalente, je me suis demandé si la distance focale était vraiment pertinente
pour caractériser une photo. Mais caractériser quoi, exactement ? Et
caractériser dans quel but ?
Je fais l'hypothèse que caractériser une photo sert à reproduire la photo,
autant que possible à l'identique, avec le même appareil ou avec un autre
appareil. Ce qu'on peut chercher alors à reproduire c'est l'angle de champ,
les distances limites de la profondeur de champ (c'est à dire la distance du
premier plan net et du dernier plan net) et le cas échéant un effet voulu de
sur- ou sous-exposition, ou de flou de mouvement. On peut décrire ces
caractéristiques par des paramètres ayant davantage de sens que le trio
focale, diaphragme et temps de pose ?
L'angle de champ est une combinaison de la distance focale et la taille du
capteur, donc indiquer seulement la distance focale en laissant le soin au
lecteur de deviner la taille du capteur en fonction du modèle de l'appareil
est possible, mais on peut faire mieux en indiquant directement la valeur de
l'angle de champ au moment de la prise de vue. Il est ensuite possible de
recréer cet angle de champ avec n'importe quelle combinaison judicieuse de
capteur et d'objectif.
De même, la profondeur de champ dépend de la distance focale, de
l'ouverture du diaphragme, de la taille des pixels du capteur et de la
distance de mise au point. Au lieu de détailler les trois premières valeurs,
on peut les combiner sous la forme de la distance hyperfocale. Les distances
des premier et dernier plans nets sont alors deux fonctions simples de la
distance de mise au point et de la distance hyperfocale. Reproduire la
profondeur de champ devient alors simplement une question de prendre la
même distance hyperfocale et de faire la mise au point sur la distance donnée.
Si le photographe ne cherche pas d'effet d'exposition particulier, la
sensibilité du capteur est une fonction des autres paramètres pour une
valeur d'exposition idéale, standard. En revanche si la photo a été
volontairement sur- ou sous-exposée, il faut indiquer la sensibilité utilisée
au moment de la prise de vue.
Le flou de mouvement enfin est particulier car il dépend du temps, et le temps
de pose est le seul paramètre qui en dépende également. Dans de cas d'une
exposition standard, le temps de pose a une valeur minimale qui dépend de
la distance focale, et on peut supposer que cette valeur sera choisie car elle
permet d'utiliser la sensibilité la plus faible possible et ainsi réduire le
bruit. En revanche si un flou de mouvement est voulu par le photographe, ou au
contraire si l'objet se déplace rapidement et que le but est de le « figer »,
il faut alors indiquer le temps de pose.
En conclusion, au lieu de caractériser une photo par le modèle d'appareil,
la distance focale, le nombre d'ouverture et éventuellement le temps de pose
et la sensibilité, on peut caractériser une image de manière plus générique et
descriptive en indiquant l'angle de champ, la distance hyperfocale, la
distance de mise au point et éventuellement la sensibilité et le temps de
pose. Bien que ces nouvelles caractéristiques soient moins connues que celles
utilisées jusqu'à présent, calculer leurs valeurs ne pose pas de problème
aux appareils photos numériques et pourraient donc être incluses dans les
métadonnées des images. Et je suis certain que la signification des
caractéristiques « classiques » n'est pas mieux comprise par la plupart des
photographes que les caractéristiques proposées ici, remplacer en ensemble de
valeurs hermétique par un autre ensemble de valeurs hermétiques ne devrait donc
pas poser de problème une fois vaincue la résistance naturelle de l'être
humain au changement.
Applications numériques
Pour se faire une idée des valeurs numériques des caractéristiques décrites
plus haut, voici des applications numériques de diverses formules pour trois
appareils photos de référence : un compact, un boitier APS-C et un plein
format avec 3 objectifs.
Appareils photo de référence
| Appareil |
Pixels |
Capteur |
Objectifs |
| A |
21,1 Mpix |
6,17×4,55 mm
(1/2,3) |
4,3-172,0 mm, f/3,3-f/6,9 |
| B |
25,0 Mpix |
23,5×15,6 mm
(APS-C) |
16 mm, f/2,8 ;
18-135 mm, f3,5-5,6 |
| C |
27,1 Mpix |
36×24 mm
(plein format) |
16-35 mm, f/4 ;
35-70mm, f/2,8;
70-200mm, f/2,8 |
Dimensions d'un pixel
| Appareil |
ε |
Surface |
Densité |
| A |
1,15 μm |
1,33 pm2 |
752 000 px/mm2 |
| B |
3,83 μm |
14,7 pm2 |
68 200 px/mm2 |
| C |
5,65 μm |
31,9 pm2 |
31 400 px/mm2 |
Angles de champ
| Appareil |
θ (rad) |
θ (°) |
| A |
1,45-0,446 |
83-2,55 |
| B |
1,45
1,33-0,208 |
83
76,2-11,9 |
| C |
1,86-1,11
1,11-0,599
0,599-0,215 |
107-63,4
63,4-34,4
34,4-12,4 |
Distances hyperfocales
| Appareil |
F (m) |
f/N (mm) |
| A |
2,01-3730 |
4,3/8-172/6,9 |
| B |
3,04-23,9
3,85-850 |
16/22-16/2,8
18/22-135/5.6 |
| C |
2,06-54,2
9,86-310
39,4-2530 |
16/22-35/4
35/22-70/2,8
70/22-200/2,8 |
Sensibilité
En admettant que les capteurs des appareils A, B et C ne diffèrent que par la
taille de leurs pixels (ce qui est loin d'être évident) et en fixant un niveau
de bruit à ne pas dépasser dans l'image obtenue, on peut comparer leur
« sensibilités » relatives.
- A est 11 fois moins sensible que B et 24 fois moins sensible que C.
- B est 11 fois plus sensible que B et 2,2 fois moins sensible que C.
- C est 24 fois plus sensible que A et 2,2 fois plus sensible que B.
On peut aussi comparer, à distance focale et temps de pose égaux, de combien
de crans il faut ouvrir ou fermer le diaphragme pour obtenir la même
exposition et le même niveau de bruit.
- A doit ouvrir de 3,5 crans par rapport à B et de 4,6 crans par rapport à C.
- B doit fermer de 3,5 crans par rapport A et ouvrir de 1,1 crans par rapport
à C.
- C doit fermer de 4,6 crans par rapport à A et de 1,1 crans par rapport à B.
Affichage
- Moniteur 16:10 24" FullHD : 2,30 Mpx ; taille d'un pixel : 405 μm
- Moniteur 16:9 32" 4k : 8,29 Mpx ; taille d'un pixel : 265 μm
- Moniteur 16:9 27" 5k : 14,8 Mpx ; taille d'un pixel : 167 μm
- Télévision 16:9 40" FullHD : 2,07 Mpx ; taille d'un pixel : 661 μm
- Télévision 16:9 55" 4k : 8,29 Mpx ; taille d'un pixel : 455 μm
- Télévision 16:9 85" 8k ; 33,2 Mpx ; taille d'un pixel : 351 μm
- Impression papier à 300 dpi :taille d'un pixel : 84,7 μm
- Impression à 300 dpi en 10×13 cm : 1,81 Mpix
- Impression à 300 dpi en 10×15 cm : 2,09 Mpix
- Impression à 300 dpi en 20×30 cm : 8,37 Mpix
- Impression à 300 dpi en 40×60 cm : 33,5 Mpix
- Impression à 300 dpi en 76×115 cm : 122 Mpix
[ Posté le 30 septembre 2019 à 08:30 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_7_conclusion.trackback
Commentaires
Aucun commentaire
Dimanche, 29 septembre 2019
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

“riisillä ja sitruunaruoholla ryyditetty”
Sitruunainen, ei miitään erikoista. Sisältää ohramallasta, riisiä ja
vehnämallasta.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 5.0% alkoholia.
[ Posté le 29 septembre 2019 à 14:49 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_kiito_2019.trackback
Commentaires
Aucun commentaire
Dimanche, 22 septembre 2019
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Tennent ]

“fruity and hoppy”
Maybe a hint of bitter almond? But not may favourite. Contains malted barley.
Tennent Caledonian Breweries, Glasgow, Scotland. 5% alcohol.
[ Posté le 22 septembre 2019 à 22:55 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Tennent/tennents_1885_lager.trackback
Commentaires
Aucun commentaire
Samedi, 21 septembre 2019
Catégories : [ Cuisine/Chocolats ]
A. Morin, Orixas 63% Brésil : grillé, assez doux
A. Morin, Yamasá 63% République Dominicaine : fruité ?
A. Morin, Chancamayo 63% : agrumes, frais
A. Morin, Pablino 70% Pérou : fleuri, légèrement acide
A. Morin, Yvan 70% Pérou : caramel, cannelle
Erithaj, Ben Tre 65% Vietnam : raisin secs, pain d'épices
Erithaj, Ben Tre 2016 70% 2 brassages : doux, un peu acide, cacaoté
Erithaj, Ben Tre 2016 70% 3 brassages : beurre, caramel
Erithaj, Lam Dong 70% Vietnam : légèrement fumé ?
Erithaj, Ba Laï 74% Vietnam : grillé
Erithaj, Ham Luong 80% Vietnam : très grillé, sec
Weiss, Ceïba 64% République Dominicaine : päte à gäteau crue
Weiss, Li Chu 64% Vietnam : très doux, vanille
Marabou. Premium Eko 70% : bonbon, très doux
Alter Eco, 75% Pérou : cacaoté, intense, doux, gâteau au chocolat
[ Posté le 21 septembre 2019 à 16:07 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Cuisine/Chocolats/chocolats_35.trackback
Commentaires
Aucun commentaire
Vendredi, 20 septembre 2019
Catégories : [ Science ]
Taille d'un point d'affichage
La notion de flou qui est importante pour la
profondeur de champ et le
flou de bougé ne dépend
pas tant de la taille des pixels du capteur que de la taille des pixels au
moment de l'affichage, que ce soit sur un écran ou sur un support physique
comme le papier. En effet, utiliser la taille d'un pixel comme taille maximale
ε d'une tache de flou donne une garantie que le flou n'est pas
perçu par le capteur et donc n'est pas enregistré dans l'image, mais puisque
l'image est destinée à être regardée par un humain, ce qui importe in fine
c'est la capacité de l'humain à percevoir le flou. On peut donc définir
une nouvelle valeur de ε utilisé dans les calculs de profondeur de
champ et de bougé en fonction de la manière d'afficher l'image.
Pour un affichage sur écran, on peut calculer la taille d'un pixel ε
(en mètres) en fonction de la diagonale D (en pouces), du format R (par
exemple 16/9) et du nombre de pixels par ligne n:
ε = 0,0254 × D√(1 + 1 / R) / n
Pour un affichage sur papier, on peut calculer la taille d'un point ε
(en mètres) en fonction de la définition de l'impression d (en points par
pouce, dpi):
ε = 0.0254 / d
Agrandissement maximal
Pour éviter les effets de crénelage lors de l'affichage, il faut aussi veiller
à ne pas afficher l'image à une trop grande taille par rapport à la résolution
de l'image numérique. En d'autres termes, le nombre de pixels N de l'affichage
ne doit pas être plus grand que le nombre de pixels de l'image (c'est à dire
du capteur si on ne retaille pas l'image). On suppose ici que l'intégralité de
l'image est affichée sur l'écran ou le papier, c'est à dire qu'on ne va pas
zoomer dans l'image.
Pour un écran, le nombre de pixels N vaut
N = n2 / R
Pour un tirage papier de densité d points par pouce, N vaut
N = 0,155 × l2d2 / R
où l est la largeur du papier et R est le rapport largeur sur hauteur.
On peut aussi calculer N en fonction de la largeur l et la hauteur h du
papier :
N = 0,155 × lhd2
[ Posté le 20 septembre 2019 à 13:06 |
1
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_6_affichage.trackback
Commentaires
Optique photo 7 : conclusion
Commentaire N° 1, Blog & White
le 30 septembre 2019 à 08:30
Lundi, 16 septembre 2019
Catégories : [ Science ]
Exposition et temps de pose
Du point de vue pratique, l'exposition d'une photo dépend du nombre
d'ouverture du diaphragme, de la sensibilité du capteur
et du temps de pose. On peut comprendre cette exposition comme la quantité de
lumière nécessaire pour que chaque pixel du capteur CCD reçoive suffisamment
de photons pour produire une valeur « raisonnable » de ce pixel. On a alors le
choix d'exposer ces pixels à un flot de lumière important pendant un temps
court, ou au contraire un flot de lumière plus faible pendant un temps plus
long pour recevoir le même nombre de photons, et donc obtenir le même
résultat.
Plus formellement, l'exposition lumineuse
H est définie par H = Et, où E est l'éclairement lumineux c'est à dire le flot
de lumière et t est le temps de pose.
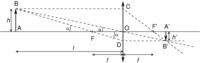
En faisant l'hypothèse d'un système idéal d'une lentille mince parfaitement
transparente uniformément éclairée par l'objet photographié, on peut
définir
l'éclairement lumineux comme E = Lπ / (4(N / (1 - f / l))2) où L
est la luminance de l'objet, f est
la distance focale de l'objectif, l est la distance de l'objet et N est le
nombre d'ouverture du diaphragme. Dans le cas courant où la distance focale
est négligeable par rapport à la distance à l'objet, on peut simplifier cette
définition en E = Lπ / (4N2).
Par ailleurs, la sensibilité
est définie par S = H0 / H où H0 est une valeur
d'exposition de référence, constante. En considérant que la luminance de
l'objet est elle aussi constante, on obtient la relation
St / N2 = 4H0 / (Lπ)
qui indique bien que si l'un des trois paramètres N, S ou t varie alors l'un
au moins des deux autres paramètres doit varier pour que l'égalité soit
toujours vérifiée.
Flou et temps de pose
Si le sujet ou l'appareil photo se déplacent pendant la prise de vue, on
comprend aisément qu'un point de l'objet donne une image qui se déplace sur le
capteur, qui enregistre alors plusieurs points contigus.
Parmi tous les mouvements possibles de l'appareil photo qui conduisent à un
flou de bougé, un mouvement simple à modéliser est une rotation de l'appareil
photo autour du centre optique O. On considère que durant la prise de vue, le
point A s'est déplacé en B, et que le temps de pose est assez long pour que le
capteur enregistre toutes les positions prises par ce point entre A' et B'.
L'image du point, au lieu d'être un point, est alors un trait de longueur h'.
On peut exprimer h' en fonction de θ
h' = tan(θ)lf/(l-f)
Lorsque la distance focale f est négligeable devant l et que θ est
inférieur à 0.5 radians (soit 29°, ce qui fait que l'erreur d'approximation de
tan(θ) est inférieure à 10%), on peut simplifier en
h' = fθ
En considérant que l'angle θ est le résultat d'une rotation de vitesse
angulaire ω durant un temps t, c'est-à-dire θ = ωt on peut
écrire
h' = fωt
En notant ε la hauteur d'un pixel et en reprenant l'hypothèse que le
flou est invisible
si la taille h' de la « tache » de flou est plus petite qu'un pixel, on peut
écrire que le flou de bougé est invisible si
t < ε/(fω)
On retrouve ici l'approximation dite « de l'inverse de la focale », à savoir
que pour éviter le flou de bouger,
« le temps de pose minimum a la même valeur
numérique que l'inverse de la distance focale exprimée en millimètres. »
Cette
approximation suppose que
ε/ω = 1/1000 m·s·rad-1. On peut
supposer que pour un photographe moyen, la vitesse ω de ses mouvements
involontaires est constante, mais on voit que cette approximation dépend
directement de la taille ε d'un pixel qui peut beaucoup varier d'un
capteur à l'autre.
[ Posté le 16 septembre 2019 à 21:22 |
2
commentaires |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_5_temps_de_pose.trackback
Commentaires
Optique photo 6 : l'affichage
Commentaire N° 1, Blog & White
le 20 septembre 2019 à 13:07
Optique photo 7 : conclusion
Commentaire N° 2, Blog & White
le 30 septembre 2019 à 08:30
Dimanche, 15 septembre 2019
Catégories : [ Science ]
Le bruit
Chaque pixel d'un capteur CCD
d'appareil photo numérique est un transducteur qui transforme une quantité de
lumière reçue Q en une différence de potentiel électrique u0 qui
est proportionnelle à Q selon un facteur f :
u0 = fQ
Dans un situation idéale, une valeur donnée de Q devrait donner
systématiquement la même valeur nominale u0. En réalité, à cause du
bruit, des mesures
répétées d'une même valeur d'exposition donneront des valeurs différentes de u
u = u0 + ε
où ε est une erreur de mesure aléatoire. Cela signifie que chaque
mesure répétée de u aura une valeur différente de ε, mais aussi que
deux pixels voisins qui sont exposés de la même manière donneront des valeurs
de u différentes.
Si on considère qui le bruit est un bruit blanc (ce qui est
probablement faux mais suffisamment similaire à la réalité pour être utile à
cette explication), alors les valeurs de ε sont couramment proches de
zéro (et donc u est proche de u0), mais ε peut parfois,
plus rarement, être nettement plus grand que zéro et donc la valeur de u est
nettement différente de u0.
La sensibilité d'un capteur numérique
Les valeurs typiques de u sont très petites et il est donc nécessaire de les
amplifier avant de les numériser. Ainsi une valeur v de pixel (typiquement entre
0 pour la valeur la plus sombre et 255 pour la valeur la plus lumineuse) est
obtenue en effectuant
v = Au si Au ≤ vmax
v = vmax si Au > vmax
où A est le facteur d'amplification. Comme la valeur de v ne peut dépasser
vmax, on comprend que si l'amplification A choisie est trop élevé
par rapport à u, l'intervalle de valeurs possibles pour un pixel n'est pas
suffisant pour représenter la valeur correcte de ce pixel, et on arrive à la
saturation.
En faisant varier A, on peut faire varier la « sensibilité » du capteur et
obtenir des valeurs élevées de v (donc un pixel très lumineux) à partir d'une
valeur faible de u (par exemple en photographiant dans une situation de faible
luminosité).
Cependant, comme v contient aussi le bruit ε, ce dernier est amplifié
de la même manière :
v = Au0 + Aε
Ainsi, plus la « sensibilité » du capteur est élevée, c'est à dire plus le
facteur d'amplification A est élevé, plus le bruit est élevé et devient
perceptible pour l'observateur.
Par exemple pour une image d'un objet noir, on s'attend à ce que v soit proche
de zéro pour tous les pixels même pour une grande valeur de A parce que
u0 est justement proche de zéro. Mais il peut arriver que ε
soit bien plus grand que u0, ce qui conduit à ce que la valeur v du
pixel soit essentiellement égale à Aε. Ceci se traduit par des pixels
brillants au milieu de pixels sombres, typiques du bruit des photos prises en
faible lumière avec une sensibilité élevée.
Comparaison de capteurs
Dans des conditions d'éclairage uniforme dans l'espace et le temps d'une
surface s pendant un temps t (le temps de pose d'une photo), on peut définir
les grandeurs suivantes :
où Q est la quantité de
lumière
c'est à dire approximativement le nombre de photons qui arrivent sur la
surface s. En combinant ces trois définitions, on obtient
Q = Hs
c'est à dire que la quantité de lumière qui arrive sur un pixel est
proportionnelle à la surface de ce pixel. Autrement dit, à exposition H égale,
un pixel plus grand reçoit une plus grande quantité de lumière qu'un pixel
plus petit.
En reprenant définition de u0 plus haut, on a
u0 = fHs
et donc, en ignorant pour le moment le bruit ε on a
v = AfHs
Ainsi, pour obtenir la même valeur v avec deux capteurs (capteur 1 et capteur
2) dont les pixels ont respectivement des surfaces s1 et
s2, on a besoin d'un facteur d'amplification A1 sur
le capteur 1 et A2 sur le capteur 2 tels que
A2 = A1s1 / s2
On a vu plus haut que le bruit est amplifié. Cela se traduit par
A2ε = A1εs1 / s2
c'est à dire que le bruit dans l'image obtenue par le second capteur est
s1 / s2 fois plus élevé que le bruit dans l'image
obtenue par le premier capteur.
Qualitativement, cela signifie que pour obtenir deux photos exposées de
manière identiques avec deux appareils différents, l'un muni d'un capteur à
grands pixels et le second muni d'un appareil à petits pixels, celui dont les
pixels sont petits a besoin d'un facteur d'amplification plus élevé et
produit donc une image plus bruitée.
Sensibilité
La sensibilité est
définie par S = H0 / H où H0 est une valeur d'exposition
de référence.
Un photographe s'attend à ce que lorsqu'on prend la même photo avec deux
appareils (dont les capteurs sont équivalents à l'exception de la taille des
pixels, et donc de leur nombre), l'image obtenue est exposée de la même façon
(en supposant que la distance focale, le nombre d'ouverture, le temps de pose
et la sensibilité sont les mêmes). Une conséquence est que les facteurs
d'amplification des deux appareils doivent être différents puisque les tailles
des pixels sont différentes, et que l'image de l'appareil dont les pixels sont
plus petits contiendra donc plus de bruit.
Réciproquement, si on cherche à produire avec les deux appareils des images
contenant une quantité de bruit identique, il faut changer les paramètres
d'exposition de l'appareil produisant le plus de bruit de sorte à
- diminuer la sensibilité S d'un facteur s1 / s2 afin
d'utiliser le même facteur d'amplification dans les deux appareils, et
- augmenter l'exposition H d'un facteur s1 / s2 afin
de compenser la diminution de la sensibilité.
On peut parvenir à ce dernier point en augmentant le temps de pose ou en
augmentant la surface de la pupille du diaphragme d'un facteur
s1 / s2.
Selon le modèle simplifié utilisé ici, à tailles de capteurs égales, un
capteur de plus haute définition (donc comportant un plus grand nombre de
pixels) produira donc des images contenant plus de bruit.
Si on décide de considérer qu'avec une exposition de référence Href
la sensibilité Sref maximale d'un capteur de référence dont les
pixels ont une surface sref représente une quantité de bruit de
référence, on peut considérer qu'à quantité de bruit identique, un capteur de
plus haute définition dont les pixels ont une surface s aura donc une
« sensibilité équivalente » Seq plus faible nécessitant une
exposition Heq. En effet
Sref = H0 / Href et
Heq = sref / sHref, donc
Seq = Srefs/sref
Il faut noter que la sensibilité équivalente, qui dépend de la surface des
pixels, n'a rien à voir avec la focale équivalente qui dépend des dimensions
du capteur et non de celles de ses pixels.
[ Posté le 15 septembre 2019 à 17:22 |
2
commentaires |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_4_sensibilite.trackback
Commentaires
Optique photo 5 : temps de pose
Commentaire N° 1, Blog & White
le 16 septembre 2019 à 21:21
Optique photo 7 : conclusion
Commentaire N° 2, Blog & White
le 30 septembre 2019 à 08:30
Traduction: [ Google ]
Catégories : [ Bière/Donut Island ]

Makea, vähän katkera, hedelmän makuinen. Sisälttää ohrasmallasta.
Valmistaja: Panimo Hiisi. 8% alkoholia.
[ Posté le 15 septembre 2019 à 13:48 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Donut_Island/donut_island_present_tense.trackback
Commentaires
Aucun commentaire
Samedi, 14 septembre 2019
Catégories : [ Science ]
Le grandissement

La hauteur h' de l'image d'un objet de hauteur h situé à une distance l d'un
objectif de distance focale f est donnée par h' = hf / l. Le rapport des
tailles entre l'objet et l'image s'appelle le grandissement γ, et en
supposant que f est négligeable devant l, γ est défini par
γ = h' / h = f / l
Le grandissement dépend donc uniquement de la distance à l'objet et de la
distance focale de l'objectif.
La perspective
On peut donner une valeur chiffrée à la perspective en comparant les tailles
des images de deux objets de même taille mais situés à des distances
différentes. En supposant que la profondeur de
champ est
suffisante pour que les images des deux objets soient nettes, on peut noter
h'1 et h'2 les hauteurs de ces images et l1
et l2 les distances des objets, puis calculer le rapport
h'1 / h'2
h'1 / h'2 = l2 / l1
On constate que le rapport des hauteurs des images dépend seulement du rapport
des distances des deux objets. En particulier, il ne dépend pas de la distance
focale de l'objectif (si cette dernière est négligeable devant les distances
aux objets).
Une conséquence de ce constat est qu'un objectif à longue focale n'« écrase »
pas davantage les perspectives qu'un objectif à courte focale (si on ignore
les déformations sur les bords de l'image dûs aux courtes focale). Cette
conclusion est cohérente avec le fait qu'un objectif à courte distance focale
associée à un capteur de petite taille donnera la même image (avec la même
perspective) qu'un objectif de plus longue distance focale associé à un
capteur plus grand (lorsque le rapport des distance focales de ces deux
objectifs est égal au crop factor des deux capteurs).
[ Posté le 14 septembre 2019 à 14:25 |
1
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_3_perspective.trackback
Commentaires
Optique photo 7 : conclusion
Commentaire N° 1, Blog & White
le 30 septembre 2019 à 08:30
Vendredi, 13 septembre 2019
Catégories : [ Science ]
Le flou
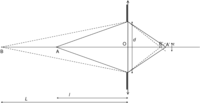
Lorsque la mise au point d'un système optique
(simplifié) a été
effectuée, l'image d'un objet ponctuel A situé à une distance l de l'objectif
est un point A'. La mise au point est cependant imparfaite pour un objet B
situé à une distance L plus (ou moins) loin que l : les rayons lumineux
convergent en B' au lieu de A', continuent leur course et vont s'étaler autour
de A' dans une zone de largeur ε. Sur le capteur d'un appareil photo,
l'image B' de B est donc une tache circulaire dont le diamètre ε dépend
de L, de la distance de mise au point l, de la distance focale f de la
lentille et du diamètre d de la pupille, c'est-à-dire le trou circulaire par
lequel la lumière entre dans la lentille, délimitée par le diaphragme. On
considère ici que la pupille est suffisamment grande pour négliger les effets
dûs à la diffraction.
On considère que l'image d'un point est net lorsque l'observateur (humain,
en général) est incapable de faire la différence entre un « vrai » point et
une tache. Le diamètre ε maximal d'une telle tache est lié au pouvoir
de séparation de l'½il de l'observateur, qui est lié non seulement à la taille
de la tache mais aussi à la distance à laquelle se situe l'observateur : plus
l'observateur est éloigné, plus il est difficile de distinguer une petite tache
d'un « vrai » point. La valeur de cet ε maximal n'est pas universelle,
car elle dépend in fine de l'affichage de la photo (sur écran ou en tirage
papier) et de la manière dont on regarde cette photo : il sera par exemple
plus facile de remarquer un flou en regardant de près une image tirée en grand
format qu'en regardant de loin une image tirée en petit format.
La profondeur de champ
D'après l'article de Wikipedia sur la Profondeur de champ, les
limites de distance où les objets donneront une image considérée comme nette,
une fois choisie un valeur ε maximale sont
L = l / (1 ± εl/df)
Les objets dont la distance est située entre ces limites auront une image
considérée comme nette, car la tache de diamètre ε est trop petite
pour être distinguée d'un « vrai » point net. On remarque que pour
photographier un objet donné situé à une distance l en utilisant un objectif
de distance focale f donnée, ces deux valeurs limites ne dépendent que du
diamètre de la pupille, et pas du tout de la taille du capteur de l'appareil
photo. Plus précisément, si les pixels du capteur sont plus grands que
ε il n'y aura aucun flou car la tache circulaire sera contenue dans un
seul pixel. Si les pixels sont plus petits que ε mais que les pixels à
l'affichage de la photo (sur écran ou sur papier) sont plus grands que la
tache circulaire, alors il n'y aura aucun flou à l'affichage, mais on pourra
voir le flou en zoomant dans l'image (ce qui revient à dire que les pixels
d'affichage deviennent plus petits que la tache circulaire).
Le nombre d'ouverture et la focale équivalente
La taille d de la pupille est exprimée dans la pratique non pas en millimètres,
mais en fraction 1/N de la distance focale de l'objectif : d = f / N. N est le
nombre d'ouverture et vaut donc N = f / d.
Si considère qu'en utilisant un objectif de distance focale f sur un capteur
de taille différente on a une distance focale équivalente feq = kf,
alors on peut écrire
N = feq / kd
où k est appelé « crop factor », soit
kN = feq / d
En introduisant la notion de nombre d'ouverture équivalent Neq
défini par Neq = kN, la formule précédente devient
Neq = feq / d
qui est a la même forme que la définition du nombre d'ouverture, mais en
utilisant le nombre d'ouverture équivalent et la focale équivalente.
Hyperfocale
On peut définir F = df/ε. En remplaçant le diamètre de la pupille d
par son expression utilisant la distance focale et le nombre d'ouverture, on
obtient
F = f2/εN
Les distances limites de la profondeur de champ deviennent alors
L = lF / (F ± l)
La distance hyperfocale F est la distance l minimale pour laquelle tous
les objets entre F/2 et l'infini sont nets. Un corrolaire est que lors d'une
mise au point à l'infini, tous les objets situés au delà d'une distance F sont
nets.
Si on utilise la distance hyperfocale comme unité de distance de mise au point
photographié, on peut représenter, de manière générique pour n'importe quelle
combinaison de capteur, distance focale et nombre d'ouverture, les distances
limites entre lesquelles les objets forment des images nettes (en supposant
toujours que la distance focale est négligeable par rapport à la distance de
mise au point).
En notant l = qF, on peut exprimer L en fonction de q et F:
L = qF / (1 ± q)

Le diagramme ci-contre indique les limites minimum et maximum de netteté pour
une mise au point égale à une fraction de la distance hyperfocale F. On remarque
que vers 0,9F, la limite maximum de netteté est déjà à 10F, et tend vers
l'infini lorsqu'on se rapproche de 1F. Si on fait la mise au point à une
valeur supérieure à F, la limite maximum de netteté reste à l'infini alors que
la limite minimale n'augmente comparativement que très peu.

Le diagramme ci-contre représente les limites de netteté pour des distances de
mise au point inférieures à 0,5F. On remarque que lors d'une mise au point à
0,5F, les objets situés au delà de F ne sont plus nets.
[ Posté le 13 septembre 2019 à 18:54 |
4
commentaires |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_2_profondeur_de_champ.trackback
Commentaires
Optique photo 3 : perspective
Commentaire N° 1, Blog & White
le 14 septembre 2019 à 14:22
Optique photo 5 : temps de pose
Commentaire N° 2, Blog & White
le 16 septembre 2019 à 21:21
Optique photo 6 : l'affichage
Commentaire N° 3, Blog & White
le 20 septembre 2019 à 13:07
Optique photo 7 : conclusion
Commentaire N° 4, Blog & White
le 30 septembre 2019 à 08:30
Mardi, 10 septembre 2019
Catégories : [ Science ]
Le modèle simplifié

On peut simplifier un objectif d'appareil photo en le considérant comme une
lentille mince de centre O et de distance focale f. L'axe optique de la
lentille passe par O et est perpendiculaire à cette dernière. Les points F et
F', situés de part et d'autre de la lentille à une distance f sont les points
focaux de cette dernière. L'objet AB, situé à une distance l de la lentille
donne alors une image A'B' sur le capteur de l'appareil photo. La hauteur de
l'objet est h et la hauteur de l'image est h'.
Les règles de l'optique géométrique sont simples :
- les rayons lumineux passant par le centre O de la lentille ne sont pas
déviés, donc AA' et BB' sont des lignes droites ;
- les rayons lumineux qui arrivent sur la lentille parallèlement à l'axe
optique ressortent de la lentille en passant par le point focal F', tel le
rayon BCB' ;
- les rayons lumineux qui arrivent sur la lentille en passant par le point
focal F ressortent parallèlement à l'axe optique, tel le rayon BDB'.
L'angle de champ
L'angle sous lequel l'objectif voit l'objet AB est l'angle θ. On a
tan θ = h / l et tan α = h / (l - f) = h' / f. On en déduit que
tan θ = (l - f)h' / lf, que l'on peut simplifier (lorsque f est
négligeable devant l) en tan θ = h' / f.
Si on considère que l'image A'B' et son symétrique (qui n'est pas représenté
sur le diagramme) sont ensemble suffisamment grands pour couvrir l'intégralité
de la diagonale du capteur, on sait que la hauteur h' de l'image représente la
moitié de la diagonale d du capteur. Cela signifie que l'angle θ est la
moitié de l'angle de champ du système objectif-capteur. On a alors
tan(angle de champ / 2) = d / 2f
Ceci montre que l'angle de champ dépend seulement de la distance focale de
l'objectif et de la taille du capteur (lorsque f est négligeable devant l,
soit en pratique lorsque la distance à l'objet est au moins dix fois plus
grande que la distance focale).
Angle de champ et taille de capteur
Pour deux capteurs de tailles différents et avec un objectif donné, le rapport
des tangentes des demi-angles de champ est égale au rapport des tailles des
capteurs. Pour des angles de champ de moins de 53° (c.-à-d. lorsque la
valeur de la tangente est proche de la valeur de l'angle, en radians), c'est
à dire lorsque la distance focale est plus grande que la diagonale du capteur,
on peut faire l'approximation que le rapport des angles de champ est égal au
rapport des tailles des capteurs, avec une erreur de moins de 10%, soit
angle1 / angle2 = diagonale1 / diagonale2
Ainsi par exemple un capteur deux fois plus grand qu'un autre capteur donnera
un angle de champ deux fois plus grand lorsque ces capteurs sont munis
d'objectifs de même distance focale.
Si on veut une approximation qui fonctionne aussi pour de grands angles, il
devient nécessaire de comparer les tangentes des demi-angles de champ, par
exemple
tan(angle1 / 2) / tan(angle2 / 2) = diagonale1 / diagonale2
ou de faire intervenir les arctangentes, par exemple
angle1 / angle2 = arctan(diagonale1 / 2f) / arctan(diagonale2 / 2f)
ce qui est nettement moins pratique à évaluer de tête.
La distance focale équivalente
Supposons que l'on a un capteur de référence dont la diagonale est
dref (par exemple un capteur 24×36 mm) et un objectif de
distance focale f.
Lorsqu'on utilise cet objectif avec un autre capteur dont la diagonale est
d, on a un angle de champ θ défini par
tan(θ / 2) = d / f
On veut alors savoir quelle serait la distance focale équivalente
feq d'un objectif fictif donnant le même angle de champ θ si
on utilisait cet objectif fictif avec le capteur de référence. On a
tan(θ / 2) = d / f = dref / feq
et donc
feq = f × dref / d
(cette valeur est correcte si f est négligeable par rapport à l et par rapport
à ld / dref).
Comparée à l'angle de champ, le calcul de la distance focale équivalente n'est
pas limitée à des angles de champ suffisamment petits. La distance focale
équivalente fait cependant appel à un facteur caché, la taille du capteur de
référence.
[ Posté le 10 septembre 2019 à 22:47 |
3
commentaires |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/optique_photo_1_angle_de_champ.trackback
Commentaires
Optique photo 2 : profondeur de champ
Commentaire N° 1, Blog & White
le 13 septembre 2019 à 18:51
Optique photo 5 : temps de pose
Commentaire N° 2, Blog & White
le 16 septembre 2019 à 21:21
Optique photo 7 : conclusion
Commentaire N° 3, Blog & White
le 30 septembre 2019 à 08:30















































© Amazon.fr
Les riches accusés du meurtre de solo sont reconnus non-coupables. Apple décide alors de se venger en rejoignant, sans prévenir ses amies, un groupe de hackers qui isolent Golden City, font périmer ses réserves alimentaires et viden...