Vendredi, 26 décembre 2014
Catégories : [ Livres/BD/Franka ]

Troisième volet du Voyage d'Ishtar.
Lors de la fête d'inauguration du yacht, Franka enquête et découvre que l'épée
peut cracher un jet d'énergie dévastateur. Le lendemain, Karat est attaqué et
tué par le feu d l'épée sur le yacht, sous les yeux de Laura. Elle part
ensuite à New York enquêter sur un riche producteur russe de cinéma qui avait
été chargé par les agents secrets russes de surveiller Karat. Franka comprend
alors que Karat a mis en scène sa mort pour échapper aux russes. Elle le
retrouve dans sa résidence du Montana, et est témoin de son assassinat par
Carmen Corazon, l'assassin qu'il avait envoyé plus tôt tuer Franka; ayant
compris que Karat fait assasiner tous ses complices, Carmen a décidé de tuer
préventivement Karat. Elle s'enfuit avec des diamants, et meurt dans
l'explosion de la voiture de Karat ayant compris que Karat fait assasiner tous
ses complices, Carmen a décidé de tuer préventivement Karat. Elle s'enfuit
avec des diamants, et meurt dans l'explosion de la voiture de Karat.
[ Posté le 26 décembre 2014 à 19:28 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Franka/la_flamme_d_argent.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Largo Winch ]

© Amazon.fr
Dix-neuvième volume de Largo Winch. Largo est la future cible de terroristes
islamistes. La jeune femme chargée de le séduire et le tuer dans un attentat
suicide est en fait une agent de la CIA. En parallèle, un père et une fille
espions séduisent miss Pennywinckle et Dwight Cochrane pour leur voler les
plans d'une pile à combustible au profit d'un mafieux russe, complice du
superviseur corrompu de l'agent de la CIA.
[ Posté le 26 décembre 2014 à 19:10 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Largo_Winch/chasse_croise.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/De cape et de crocs ]

© Amazon.fr
Onzième volume de De cape et de crocs. Eusèbe est envoyé par son père pour
devenir garde du Cardinal. Naïf, il se fait voler, puis devient l'ami d'un
poète avant de rejoindre finalement les gardes du cardinal, où il se fait
piéger puis chasser des Gardes. Frère jumeau du roi de la cour des miracles
(sans le savoir), il arrête une embuscade lors d'un déplacement du Roi,
destiné à salir l'honneur de comte de Limon, chef de la police, qui tente de
devenir le remplaçant du Cardinal. Eusèbe est alors kidnappé et amené à son
frères.
[ Posté le 26 décembre 2014 à 19:03 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/De_cape_et_de_crocs/vingt_mois_avant.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Atalante ]

© Amazon.fr
Septième volume d'Atalante, paru en 2014.
Atalante libère le géant, mais Hadès s'y oppose. Il accepte finalement de le
libérer si Atalante résout le problème des morts-vivants qui apparaissent en
Enfer que sur lesquels Hadès n'a aucun contrôle. Elle rencontre finalemet le
dernier des Grands Anciens, présent sur Terre avant l'avènement des géants et
des cyclopes, et dont les cauchemares prennent forment, donnant naissance aux
morts-vivants. Atalante tue le Grand Ancien, faisant immédiatement disparaître
les morts-vivants et guérissant Raxos. Entre temps, Hérakles libère le géant,
qui aide Atalante et ses amis à réparer l'Argos. Les aventuriers arrivent
alors là où la toison d'or est gardée. Le roi les invite à un banquet et leur
présente sa fille Médée. Cette dernière séduit Jason et lui demande de
l'emmener avec eux.
[ Posté le 26 décembre 2014 à 18:52 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Atalante/le_dernier_des_grands_anciens.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Troy ]

© Amazon.fr
Le fils du père Grommël tombe amoureux de Waha. Il mentionne les cadeaux
distribués aux enfants, et Gnondpom et Tyneth veulent les leurs. Tous les
quatre partent alors au Pölnör. À leur arrivée, les deux enfants détruisent le
palais du père en Grommël parce qu'on refuse de leur donner des cadeau. Les
quatre voyageurs retournent alors en ville à la rencontre du père Grommël qui
fait sa tournée, mais ils découvrent qu'ils ne peuvent avoir de cadeau que
s'ils écrivent d'abord une lettre, qu'ils font écrire par un écrivain public ;
ce dernier indique cependant que les enfants ont été très méchants et ne
méritent pas de cadeau. Ils mettent la lettre à la boite puis grâce au
traineau magique, retournent au village troll la veille. La mère fouettarde
apparaît alors au lieu du père Grommël, mais elle se fait dévorer.
[ Posté le 26 décembre 2014 à 18:42 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Troy/pas_de_nol_pour_le_pere_grommel.trackback
Commentaires
Aucun commentaire
Catégories : [ Livres/BD/Blake et Mortimer ]

© Amazon.fr
Vers la fin de la seconde guerre mondiale, Blake est transféré de l'armée de
l'air vers les services secrets pour piloter un futur prototype. Il apprend
que l'empereur Basam-Damdu s'arme en secret dans l'Himalaya et attend que les
deux camps s'épuisent pour envahir le monde. À la base secrète de Scaw-Fell,
il rencontre Mortimer, qui lui présente les plans du futur Espadon. Ils se
rendent ensuite à Bletchley Park, où ils rencontrent Olrik, spécialiste des
langues slaves. Ils sont espionnés et des plans sont volés. Blake et Mortimer
se rendent ensuite à Gibraltar pour mettre en place des leurres contre les
U-Boots conçus par Mortimer. Ils découvrent un espion qui communique avec
Olrik via son frère jumeau au QG de Londres. Olrik s'enfuit à Lhassa tandis
que le gouvernement britannique refuse d'intervenir au Tibet.
[ Posté le 26 décembre 2014 à 18:24 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Blake_et_Mortimer/le_baton_de_plutarque.trackback
Commentaires
Aucun commentaire
Mardi, 16 décembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma/The Hobbit ]

Wikipedia
After having been woken up by Bilbo in in The Desolation of Smaug,
Smaug attacks Laketown. He is defeater by Bard, who leads the survivors to the
Dale, while the dwarves who had stayed at the town rejoin Thorin, Bilbo and
the other inside the Lonely Mountain. Thorin has gone mad because the gold is
tainted by the dragon and because he cannot find the Arkenstone (actually
found and kept hidden by Bilbo); he also refuses to help the human refugees.
Meanwhile, Gandalf is saved from Dol Guldur by Galadriel, Elrond and Saruman;
Sauron is sent back to Mordor. Overnight, an army of Elves appears in front of
the gates of the Kingdom under the Mountain, demanding their share of its
treasures. Because of Thorin's refusal to share anything, the humans side with
the Elves and are about to attack when King Dain arrieves with an army of
dwarves. Gandalf finally joins them, announcing that the orcs, lead by Azog
are about to attack. Nobody cares to believe him until the orcs actually
attack. The allies are outnumbered but Thorin is finally convinced by Bilbo to
walk out of the mountain and lead the dwarves. With a few other dwarves, they
attempt to bring down Azog, who is coordinating the attack from Ravenhill.
They are however ambushed by Bolg, who has been leading a second army of orcs.
Azog and Bolg are finally killed, but Thorin is killed as well. The orcs now
being defeated, Gandalf and Bilbo travel back to the Shire.
[ Posté le 16 décembre 2014 à 23:45 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/The_Hobbit/the_hobbit_the_battle_of_the_five_armies.trackback
Commentaires
Aucun commentaire
Samedi, 13 décembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Titanic ]

“Maris Otter pale malt and fine wheat malt”
Just another ale, barely bitter. Contains malted barley and wheat.
Titanic Brewery. Burslem, Stoke-on-Trent, England. 4.1 % alcohol.
[ Posté le 13 décembre 2014 à 22:41 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Titanic/titanic_iceberg.trackback
Commentaires
Aucun commentaire
Mardi, 2 décembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Science ]
Let's consider base 10 logarithms and the basic equality
log(a×b) = log(a) + log(b)
Rounding to two places after the decimal separator, we also start with
log(2) = 0.30
and
log(10) = 1
Therefore, we have
log(4) = 2⋅log(2) = 0.60
and
log(8) = 3⋅log(2) = 0.90
Also,
log(10) = log(2) + log(5) = 1
therefore
log(5) = 0.70
Then a bit more approximation: 81 ≈ 80, therefore
2⋅log(9) ≈ log(10) + log(8)
This gives us
log(9) ≈ 0.95
and
log(3) = log(9)/2 = 0.48
as well as
log(6) = log(2) + log(3) = 0.78
In the same way, 50 ≈ 49, therefore
log(5) + log(10) ≈ 2⋅log(7)
in other words,
log(7) ≈ 0.85
With more approximations, one will find the logs of more prime
numbers without the need for a calculator.
[ Posté le 2 décembre 2014 à 00:02 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Science/compute_logarithms_in_your_head.trackback
Commentaires
Aucun commentaire
Samedi, 29 novembre 2014
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

Kukkatuoksuinen lager olut. Sisältää ohraa.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 4.5% alkoholia.
[ Posté le 29 novembre 2014 à 23:45 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_keito.trackback
Commentaires
Aucun commentaire
Vendredi, 28 novembre 2014
Catégories : [ TV/Cinéma ]

boxofficestory.com
Rita trahit son fiancé Fred, gangster ayant volé une fortune en lingots, au
profit de M. Charles qui lui a promis la moitié du magot. Ce dernier la trahit
cependant à son tour. Rita décide alors de raconter son histoire (embellie) à
sa tante Léontine, qui remonte à Paris pour punir Charles. Rita rencontre
Tiburce, le neveu de Charles et en tombe amoureuse, ce qui retient Léontine de
froidement assassiner Charlse. Ce dernier, suite à des négociations avec
Léontine, vend l'or contre du liquide, pour acheter la paix entre elle et
lui, mais les billets étant des bolivars, personne ne veut les reprendre
(surtout que Léontine a empêché la transaction). De son coté, Fred essaye de
récupérer son magot et fini perdu dans un sous-terrain. Le jour du mariage,
Rita dit « non » à la mairie, et Léontine finit par assassiner Charles.
[ Posté le 28 novembre 2014 à 23:45 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/faut_pas_prendre_les_enfants_du_bon_dieu_pour_des_canards_sauvages.trackback
Commentaires
Aucun commentaire
Dimanche, 23 novembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Irene Adler is killed by Moriarty after having failed to deliver a letter that
Holmes had intercepted. Holmes, investigating apparently unrelated crimes
commited by Moriarty's gang, meets Simza, the recipient of the letter, at
Watson's bachelor party, and prevents her assassination. After Watson's
wedding, Holmes meets Moriarty, and the latter threatens to kill the young
couple if Holmes continues interfering in his business. Watson and Holmes
follow Simza to Paris, looking for her brother Rene, sender of the letter.
They discover that the anarchist group to which Rene used to belong had been
forced to place bombs for Moriarty. Holmes incorrectly deduces the presence of
a bomb at the Opera, while it was actually at an hotel, where the explosion
was meant to cover the assassination of Alfred Meinhard by a sniper. Ther
latter's death grants Moriarty ownership of Meinhard's arms factory in
Germany. Holmes and his companions travel there following clues in Rene's
letter. Holmes, captured and tortured by Moriarty, describes his plot to start
a war in Europe after becoming the owner of various industries that would
become very profitable in a war. Watson frees Holmes and they then traver to
the peace conference in Reichenbach, Switzerland, the logical place where an
assassination by Moriarty would start a war. Simza and Watson manage to
identify Rene, disguised as one of the ambassadors and prevent the
assassination, while Holmes fights Moriarty on a balcony. Holmes, injured,
cannot win the fight, so he decides to throw himself and his opponent into the
waterfall below. In the end, Holmes is presumed dead, but Watson receives a
parcel that indicates he is actually still alive.
[ Posté le 23 novembre 2014 à 11:56 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/sherlock_holmes_a_game_of_shadows.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Harviestoun ]

“Aged in selected oak casks formerly used to mature Highland Park's … 12
Year Old Single Malt Scotch Whisky”
A dark ale, very sweet, with a chocolate aroma and coffee-like bitterness.
Contains barley and oats.
Harviestoun Brewery, Alva, Clackmannanshire, Scotland. 8% alcohol.
[ Posté le 23 novembre 2014 à 11:31 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Harviestoun/harviestoun_ola_dubh.trackback
Commentaires
Aucun commentaire
Dimanche, 16 novembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
The Pirate Captain once again hopes to get the Pirate of the Year Award, but
gives up when he seens how much plunder his opponents have gathered. He then
attacks severa ships, none of which contained any riches, until he meets
Charles Darwin. The latter recognizes the Captain's parrott for what it really
is: a dodo bird, a species long extinct. Darwin wants to present the bird to
the royal society but the Captain insists on presenting it himself, and the
pirates travel to Victorian London where the Queen hates pirates. After
a failed attempt to steal the dodo by Darwin's “manpanzee” butler, the
pirates disguised as scientists present the dodo to the Royal Society. They
are soon after identified as pirates, but the Queen eventually exchange the
the dodo for a large treasure, which allows the captain to win the Pirate
of the Year Award; his royal pardon is however discovered and he is banished.
The crew soon discovers the disappearance of the dodo, feeling betrayed,
abandon the Captain in London, where he lives as a peddler. One day at the
zoo, he meets Darwin in front of the dodo's empty cage, and learns that the
Queen is part of a secret society of the world's most powerful people who eat
extremely rare animals for dinner. With Darwin, the Captain boards the Queen's
steamboat and after a long battle eventually sink the ship, saves the dodo and
regain the trust of his crew which had arrived just in time to save them.
[ Posté le 16 novembre 2014 à 11:07 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/the_pirates.trackback
Commentaires
Aucun commentaire
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

“hedelmäinen aromi”
Aika hedelmäinen ja sitruunainen. Sisältää ohraa.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 4.5% alkoholia.
[ Posté le 16 novembre 2014 à 10:43 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_rakki.trackback
Commentaires
Aucun commentaire
Dimanche, 9 novembre 2014
Traduction: [ Google ]
Catégories : [ Bière/Hiisi ]

Aika makea, maistuu paahteisella. Se sisältää lakritsijuurta, mutta en
huomannut että se maistuu lakritsilla. Sisältää ohraa.
Panimoyhtiö Hiisi, Jyväskylä, Suomi. 4.5% alkoholia.
[ Posté le 9 novembre 2014 à 19:21 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Hiisi/hiisi_kiira.trackback
Commentaires
Aucun commentaire
Dimanche, 2 novembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Theakston ]

Quite sweet stout, slightly fruity. Contains barley and wheat.
T&R Theakston Ltd., Masham, North Yorkshire, England. 5.6% alcohol.
[ Posté le 2 novembre 2014 à 11:27 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Theakston/theakston_old_peculier.trackback
Commentaires
Aucun commentaire
Dimanche, 26 octobre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma/Marvel ]

Wikipedia
In 1942, Steve Rogers wants to fight in the war, but is unfit for duty. Being
smart, he is eventually accepted in a special unit and accepts to be the
guinea pig for an experiment. His body is enhanced and gains superhuman
abilities. The scientist who conducted the experiment is killed by a spy soon
after, but Rogers manages to catch the spy. The latter works for Hydra,
an organization originally working for Hitler and researching supernatural
phenomena. Its head, Schmidt, the first guinea pig for body enhancement, has
found an infinite source of energy and has built new weapons in order to take
over the world. Now stronger, Rogers wants to fight in the war but he is
instead ordered to perform in a show promoting war bonds, as character Captain
America. While touring on the front, Rogers learns his friend has been
captured by Hydra and attacks alone their base and frees the prisoner.
With the help of Howard Stark, he becomes Captain America the super soldier,
armed with an indestructible circular shield. Along with a small group of
soldiers, they attack other Hydra bases. They eventually manage to capture
Schmidt's mad scientist and locate Hydra's last base, from which Schmidt plans
to attack American cities with a gigantic wing-shaped airplane. Rogers manages
to board the airplane, fights Schmidt, removes its magical power supply and
crash lands in the Arctic and is considered lost. 70 years later the crash
site is dicovered and Rogers, who was asleep, awakes in the modern world where
he joins S.H.I.E.L.D.
[ Posté le 26 octobre 2014 à 23:45 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/Marvel/captain_america.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Shepherd Neame ]

“bittered with locally grown Fuggles hops”
Quite bitter, with a not-so-nice metallic taste on the first sip. Contains
barley malt.
Shepherd Neame Ltd., Faversham, Kent, England. 6.1% alcohol.
[ Posté le 26 octobre 2014 à 11:06 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Shepherd_Neame/shepherd_neame_india_pale_ale.trackback
Commentaires
Aucun commentaire
Samedi, 18 octobre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Brewdog ]

“citrous and resinous flavours… Columbus [hops]… citrus… Ahtanum
[hops]… tropical fruits… rye adds a spicyness to the specialty malt
caramel… ginger flavour… orangey, biscuity, almost chocolately”
Strong orange flavours and grapefruit bitterness. Contains malted
barley.
BrewDog plc, Ellon, Aberdeenshire, Scotland. 4.5% alcohol
[ Posté le 18 octobre 2014 à 21:10 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Brewdog/brewdog_alpha_pop.trackback
Commentaires
Aucun commentaire
Samedi, 11 octobre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Clanconnel ]

“Biscuit notes… grapefruit bitterness… citrus and floral aroma”
Just another ale. Contains barley malt and wheat.
Clanconnel Brewing company, Craigavon, Northern Ireland. 4.4% alcohol.
[ Posté le 11 octobre 2014 à 23:21 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Clanconnel/mcgrath_s_irish_pale_ale.trackback
Commentaires
Aucun commentaire
Dimanche, 5 octobre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Livres ]

© Amazon.fr
On a parallel-universe Earth named Arbre, thinkers are named avouts and
live in concents, closed, monastery-like communities with a strict
discipline, that open to the outside world only once every year, decade,
century or millenium, depending on the group they belong to. The narrator,
Erasmas, lives in such a community. When his mentor Orolo is thrown out of the
concent with no explanation, he starts to investigate with the help of a few
friends and eventually finds out that Orolo had discovered that a spacehip is
orbiting around Arbre. Soon after, he, his friends and several other are told
to leave the concent and go across the world to another concent. With the help
of family and friends from the outside world, Erasmas decides to take a detour
to try and find where Orolo has gone. After a long trip across the North pole
(the shortest route) he finally finds Orolo on a tropical island, at a place
that works like a concent without being one, where the people had been
excavating for hundreds of years a burried temple. Soon after, a space capsule
lands on the site, containing the corpse of a woman who obviously comes from
the spaceship, and is identified from her body's chemistry that she doesn't
belong to this universe. The digging site is soon after destroyed from orbit
by the spaceship and, Orolo being dead, Erasmas decides to continue his
journey to the concent where he was supposed to go. There avouts and ordinary
people are brainstorming about the spaceship and what do to about it. Erasmas
discovers that an alien from the spaceship is already among them, pretending
to be an avout from a little-known concent. He explains that the spaceship has
crossed parallel universes already four times and is inhabited by people from
four parallel planets, one of them being Earth, divided into two opposed
factions, one of which plans to raid Arbre for the resources necessary to
reparing their spaceship, while the other is open to negociations. Erasmas,
his friends and a small group of avouts specialized in martial arts are sent
to be quickly trained as astronauts and soon after launched into space with a
mission to disable the bomb that threatens Arbre. After entering the
spaceship, Erasmas experiences multiple parallel possible outcomes of his
story. In the last one, he wakes up in a hospital, then takes part in
negociations between Arbre and the people of the spaceship. In the epilogue,
avouts are not anymore restricted to live in concents, starting a new era in
the history of Arbre.
[ Posté le 5 octobre 2014 à 15:25 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/anathem.trackback
Commentaires
Aucun commentaire
Dimanche, 28 septembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Greene King ]

“… Pale and Crystal malts as well as American Chinook hops… grapefruit
hop character”
Just another ale, quite nice but maybe a tad too bitter. Contains malted
barley and rye.
Morland Brewing, Bury St. Edmunds, Suffolk, England. 4.2% alcohol.
[ Posté le 28 septembre 2014 à 15:04 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Greene_King/morland_old_hoppy_hen.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Tintin buys a model ship at the flea market, that several people try to buy
from him. After being broken in a fight between Snowy and a cat, the ship gets
stolen and Tintin investigates Sakharine, one of the insistent buyers who
happen to own a replica of the same ship. Back at his place, Tintin finds a
scroll, that was hiddent in the ship. Tintin is soon after abducted by
Sakharine and taken prisoner on board of the freighter SS Karaboudjan. During
his escape, Tintin meets Haddock, the ship's captain, a drunkard who is also
prisoner of Sakharine; Tintin also discovers that Sakharine is heading to
Bagghar where the third model ship is owned by Omar ben Salaad. They escape on
a lifeboat, are gunned by a seaplane from the freighter; they manage to steal
the plane and evetually crash in the Sahara desert, where Haddock starts
telling the story of his ancestor, Sir Francis Haddock, captain of the
Unicorn, transporting a fortune in gold. The ship was boarded by Red Rackham's
pirates but the captain managed to make it explode after having taken a small
part of the treasure with him. Three model Unicorn ships contain each a
scroll which, when combined, would lead to the treasure. Tintin and Haddock
are rescued from the desert by French légionnaires; they eventually reach
Bagghar where the Castafiore is having a recital for ben Salaad. Her voice
breaks the bullet-proof glass case containing the model ship and Sakharine
then steals it. A lengthy chase ensues but Sakharine escapes with the scrolls.
Thanks to Thomson and Thompson, they reach Europe before Sakharine and attempt
to arrest him when he leaves his ship. After another lenghty fight, Sakharine, who
reveals being the descendent of Red Rackham, is finally arrested. Haddock and
Tintin following the scrolls' indications, finally find the treasure in a
hidden cellar of Marlinspike's castle.
[ Posté le 28 septembre 2014 à 15:00 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/the_adventures_of_tintin.trackback
Commentaires
Aucun commentaire
Samedi, 13 septembre 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Gru is a super-villain who plans to steal the moon. For that purpose, he needs
the shrinking ray that his opponent, Vector, stole from him. His attempts to
enter Vector's fortress fail until he notices three little orphan girls
selling cookies whom Vector invites in. Gru then adopts the three girls and
uses them to introduce himself into Vector's house and steal back the shrinking
ray. He then builds the rocket that will take him to the moon, but gets
distracted by the three girls whom he slowly grows fond of; his associated mad
scientist forces him to return the girls to the orphanage. He then flies to
the moon, reduces it and steals it, and darts back to Earth in the hope of
arriving in time for the girl's ballet recital. But the girls have been
kidnapped by Vector who wants to exchange them for the Moon. The latter takes
the moon but flies away with the girls. Gru chases them, noticing that the
Moon is growing quickly back to its original size, eventually shooting back
into its orbit, taking Vector with it. In the end, Gru definitely adopts the
girls.
[ Posté le 13 septembre 2014 à 20:54 |
1
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/despicable_me.trackback
Commentaires
Despicable Me 2
Commentaire N° 1, Blog & White
le 14 février 2016 à 12:48
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Carlow ]

“malt body… southern hemisphere hop aroma”
Very bitter, and with a metallic taste on the first sip. Contains malted
barley and wheat.
Carlow Brewing Company, Carlow, Ireland. 4.3% alcohol.
[ Posté le 13 septembre 2014 à 20:43 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Carlow/o_hara_s_amber_adventure.trackback
Commentaires
Aucun commentaire
Samedi, 30 août 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Greene King ]

“citrus finish… pale malt and Cascade and First Gold hops”
Just another pale ale, but a nice one. Contains malted barley.
Greene King, Bury St. Edmunds, Suffolk, England. 4.2% alcohol.
[ Posté le 30 août 2014 à 23:53 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Greene_King/greene_king_st_edmund_s.trackback
Commentaires
Aucun commentaire
Dimanche, 24 août 2014
Traduction: [ Google | Babelfish ]
Catégories : [ TV/Cinéma ]

Wikipedia
Jimmy Tong, the fastest taxi driver in town, is hired to be the driver of the
mysterious Clark Devlin who happens to be a secret agent. When Devlin is
seriously wounded, he tells Jimmy to continue his mission to investigate the
Banning Corporation who plans to take over the world's drinking water supply
to sell its own brand of bottled water. Jimmy wears Devlin's special tuxedo
that gives him extraordinary physical abilities. Together with his partner
Delilah Blaine (who thinks for quite some time that Jimmy is Devlin), they
find Banning's laboratory where the villain breeds waterstriders that would
pollute the water supplies with bacteria that instantly dehydrate their
hosts. They manage to stop the plot in the nick of time.
[ Posté le 24 août 2014 à 23:45 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/TV/Cinema/the_tuxedo.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Thornbridge ]

“citrus and pine aromas…roasted hazelnut, toffee and caramel malt”
I don't know about citrus and pine, I found it rather flowery. Anyway, a very
nice ale. Contains malted barley and wheat.
Thornbridge brewery, Bakewell, Derbyshire, England. 4.5% alcohol.
[ Posté le 24 août 2014 à 12:42 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Thornbridge/thornbridge_sequoia.trackback
Commentaires
Aucun commentaire
Samedi, 16 août 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Wychwood ]

“malty amber ale… fruity hop”
Just another ale. Contains barley malt.
Marston's PLC, Wychwood Brewery, Witney, Oxfordshire, England. 4.3% alcohol.
[ Posté le 16 août 2014 à 20:52 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Wychwood/wychwood_pile_drivert.trackback
Commentaires
Aucun commentaire
Samedi, 9 août 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Little Valley ]

“double hopped… strong malty taste”
Citrusy and a bit bitter. Contains barley malt and wheat malt.
Little Valley Brewery, Hebden Bridge, West Yorkshire, England. 6.0% alcohol.
[ Posté le 9 août 2014 à 21:17 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Little_Valley/little_valley_python_ipa.trackback
Commentaires
Aucun commentaire
Samedi, 2 août 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Green's ]

“brewed from naturally glute-free crops”
Suprisingly strong grapefruit and citrus taste, quite bitter. Contains millet,
buckwheat and sorghum.
Brewed in Belgium. 5% alcohol.
[ Posté le 2 août 2014 à 21:46 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Green_s/green_s_ipa.trackback
Commentaires
Aucun commentaire
Traduction: [ Google | Babelfish ]
Catégories : [ Bière/Greene King ]

“a lasting fruity flavour… inspired by the bold american pale ales”
Quite fruity, not too bitter. Contains malted barley and wheat.
Greene King, Bury St. Edmunds, Suffolk, England. 4.0% alcohol.
[ Posté le 2 août 2014 à 11:59 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Biere/Greene_King/greene_king_yardbird.trackback
Commentaires
Aucun commentaire
Mardi, 22 juillet 2014
Traduction: [ Google | Babelfish ]
Catégories : [ Livres ]

© Amazon.fr
In a not-too-distant future, the USA have become a patchwork of
privately-owned districts and highways where the law doesn't exist anymore and
the Mafia is just another business organization (focusing on home-delivered
pizzas that are always on time; if not, the Don himself apologizes in person).
In the Metaverse, a world-wide virtual reality system, Hiro, a hacker,
investigates a computer virus that affects also the human brain of hackers.
Thanks to information gathered by the associate of his former girlfriend, Hiro
learns that the virus reprograms the hackers' brains, returning it to the
state it was in Sumerian times, when there was a unique language and most
people were nothing more than robots executing programs useful to the society,
controlled by the local priest. The myth of the Tower of Babel would then come
from the event were such a priest, Enki, programmed people to speak different
languages, making them immune to the programming. In the meanwhile Y.T., a
young kourier on skateboard, friend of Hiro's, is helping the Mafia to get
their hands on a sample of the virus (that also has a biological form),
distributed as a drug by a cult. Y.T. is then abducted by the cult and taken
to the Raft, a large bunch of ships attached together around the
aircraft-carrier Enterprise, bought by the telecommunication mogul Rife. The
latter is the one who dug out clay tablets containing the virus and made a
computerized equivalent that can be absorbed by hackers through sight. Most of
the people infected by the virus are on the Raft, soon to be debarked in
California to take over North America. Hiro manages to come abord the Raft and
fails to save Y.T., but manages to get the Babel tablet (that Rife owned too)
and deprogram everybody that was infected. Y.T., in Rife's helicopter flies to
Los Angeles, where they are ambushed by the Mafia. Y.T. is the only one that
manages to escape the fight. Meanwhile in the Metaverse, Hiro manages to
prevent a massive outbreak of the Virus disguised as a light-and-sound show.
[ Posté le 22 juillet 2014 à 14:53 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/snow_crash.trackback
Commentaires
Aucun commentaire
Vendredi, 18 juillet 2014
Catégories : [ Jeux ]

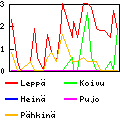
Voici le circuit millésime juillet 2014, tout en virages, il n'est pas facile
à parcourir. Cette année, les voitures rouge et bleue sont devenues poussives
vers la fin des vacances. Difficile de savoir si le problème vient d'un
mauvais contact entre les rails et la voiture, des balais ou d'un frottement
mécanique (au niveau de l'axe du moteur ?). Un patin de la rouge s'est percé à
force de frotter contre les rails, je l'ai réparé en y mettant un peu d'étain
à souder (et comme il s'agit d'un alliage à 60% de plomb, ça doit polluer un
peu en prime…)
[ Posté le 18 juillet 2014 à 13:22 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Games/circuit_auto_ete_2014.trackback
Commentaires
Aucun commentaire
Vendredi, 11 juillet 2014
Catégories : [ Livres/BD/Special Branch ]

© Amazon.fr
En 1892, Buffalo Bill présente son Wild West Show à Londres. Un ancien
officier américain est assassiné et tous les indices pointent vers un des
Sioux du spectacle, dont la famille avait été massacrée par les troupes de
l'officier ; ces indices sont cependant trop grossiers pour être crédibles.
L'indien lui-même est laissé pour mort dans l'East-End et recueilli par une
triade chinoise. Ces derniers mettent la main sur des gangsters anglais et
l'indien reconnait deux d'entre-eux. Il fait parvenir un message à Buffalo
Bill qui aide les agents de la Special Branch dans leur enquête. L'assassin,
chef de gang anglais, est arrêté et avoue avoir été engagé par le beau-frère
de la victime qui voulait prendre le contrôle de la fortune de ce derner.
[ Posté le 11 juillet 2014 à 20:36 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Special_Branch/londres_rouge.trackback
Commentaires
Aucun commentaire
Mercredi, 9 juillet 2014
Catégories : [ Livres/Ji ]

© Amazon.fr
Quatrième et dernier tome des Gardiens de Ji par Pierre Grimbert. Les
héritiers arrivent dans une reproduction de Dara quelque part dans les
montagnes, où ils retrouvent Nol l'Étrange et certains des enfants de Dara,
réincarnés en humains. Damián comprend que le Jal a été crée par accident
par les Éthèques qui expérimentaient avec une magie de plus en plus puissante.
Ils sont attaqués la nuit par les démons réincarnés en monstres, et grâce à
Nol, mortellement blessé, ils passent la porte et le retrouve dans le Lus'An.
Faits prisonniers par les Zües, ils s'allient avec elles pour repousser une
attaque des mercenaires de Saat ; ce dernier est parvenu à sortir de Karu au
moment de sa disparition et veut maintenant conquérir le monde. Sa présence
est la raison pour laquelle la disparition du Jal est imparfaite. Les
héritiers partent alors avec les Zües à l'attaque de son repaire. Grâce à
Lorilis qui a compris dans une vision comment leurs parents ont disparu (en
créant un nouveau Jal grâce à la magie), ils emportent Saat avec eux dans le
nouveau Jal où ils retrouvent leurs parents et Souanne, réincarnation de
l'esprit d'Eurydice, libère enfin l'âme de Saat. Au moment de quitter ce
nouveau Jal par la dernière Porte, Najel renonce à tuer Guéderic, incarnation
de Sombre, refusant d'accomplir la prophétie d'Usul, un dieu qui n'existe
plus. Finalement les héritiers, jeunes et vieux, se retrouvent sur l'île de
Ji, à attendre que passe un navire.
[ Posté le 9 juillet 2014 à 20:10 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/Ji/les_venerables.trackback
Commentaires
Aucun commentaire
Samedi, 5 juillet 2014
Catégories : [ Livres ]

© Amazon.fr
Peu après les événements décrits dans L'alchimiste des ombres,
les Lames tentent de remonter la piste du dragon qui a attaqué la prison du
Chatelet et tué l'Alchimiste (ainsi qu'un membre des Lames). Ils retrouvent
l'Italienne, qui sert d'intermédiaire entre un envoyé du Pape et un
prisonnier, agent de la Griffe Noire, mais ils sont attaqués et le prisonnier
est tué. L'Italienne révèle qu'elle aussi (en plus du capitaine des Lames)
travaille pour les Gardiens, un groupe de dragons qui cherchent à empêcher une
guerre entre humains et dragons. Les Lames ont cette fois-ci affaire à une
loge rebelle de La Griffe Noire qui se fait appeler les Arcanes, dont le
dirigeant veut provoquer la guerre et asservir les humains. Pour ce faire il
prend le contrôle d'un dragon Archaïque et le fait voler sur Paris dans le but
d'y provoquer un gigantesque incendie et le chaos. Un ordre religieux, les
Chatelaines, utilisent leurs connaissances de la magie draconique pour
repousser l'attaque, mais c'est seulement grâce à une Lame, la seule femme du
groupe qui a été une novice de l'ordre, avait renoncé à prononce ses voeux et
qui prend maintenant le voile, que le dragon est battu. On apprend que la
reine avait été contaminée par l'essence des dragons étant enfant, et que
ce sont les Chatelaines qui ont fait leur possible pour l'empêcher d'avoir un
enfant.
[ Posté le 5 juillet 2014 à 20:39 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/le_dragon_des_arcanes.trackback
Commentaires
Aucun commentaire
Vendredi, 4 juillet 2014
Catégories : [ Livres/BD/Leo Loden ]

© Amazon.fr
Vingt-deuxième album de Léo Loden. Léo est approché par un mafieux russe de
St. Tropez pour éliminer la concurrence locale. Devant son refus, le russe
enlève Marlène et sa mère. Léo et tonton contactent alors la mafia corse du
coin, attaquent et détruisent la villa du russe et libèrent les otages.
[ Posté le 4 juillet 2014 à 12:42 |
pas de
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/BD/Leo_Loden/tropezienne_dum-dum.trackback
Commentaires
Aucun commentaire
Mercredi, 2 juillet 2014
Catégories : [ Livres ]

© Amazon.fr
Un mois après les événement décrits dans Les lames du cardinal,
les agents de Richelieu ont pour mission d'approcher l'Italienne, une espionne
qui affirme avoir des informations sur un complot contre le trône de France
impliquant l'alchimiste des ombres, un dragon qui cherche à destabiliser le
royaume. L'Italienne veut échanger ces informations contre un pardon et
l'immunité, chose que le roi ne peut lui accorder sans provoquer de scandale.
Elle finit tout de même par lacher une information qui permet aux Lames
d'identifier parmi les membres de la conjuration la reine et la duchesse de
Chevreuse, toutes deux opposées au roi. Ce derner a pour projet secret de
faire arrêter la reine, la duchesse et le garde des Sceaux (amant de la
duchesse) à la fin d'une fête donnée au chateau de Dampierre. Les Lames
découvrent que la Griffe Noire est impliquée dans la conspiration, et que sous
couvert de pratiquer un rituel de magie draconique sur la reine afin
d'augmenter sa fertilité (cette dernière n'ayant toujours pas donné d'héritier
au trône), l'alchimiste des ombres, se faisant passer pour un maître de magie
bénéfique, tente d'enlever la reine. Les Lames réussisent à empêcher
l'enlèvement et à capturer l'alchimiste ; peu après, Paris est attaqué par un
immense dragon noir.
[ Posté le 2 juillet 2014 à 22:45 |
1
commentaire |
lien permanent ]
Adresse de trackback
https://weber.fi.eu.org/blog/Livres/l_alchimiste_des_ombres.trackback
Commentaires
Le dragon des Arcanes
Commentaire N° 1, Blog & White
le 5 juillet 2014 à 20:39












































Wikipedia
A sequel to Despicable Me. An unknown villain has stolen a powerful mutagen. Gru is hired by the Anti-Villain League and partners with Lucy to spy on the shops in a mall, where the villain is believed to be hiding. Gru suspects Mexican restaura...