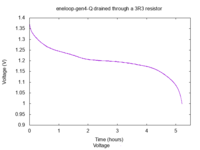
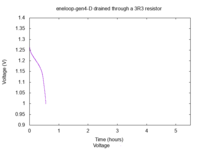
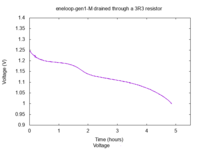
Le bruit
Chaque pixel d'un capteur CCD
d'appareil photo numérique est un transducteur qui transforme une quantité de
lumière reçue Q en une différence de potentiel électrique u0 qui
est proportionnelle à Q selon un facteur f :
u0 = fQ
Dans un situation idéale, une valeur donnée de Q devrait donner
systématiquement la même valeur nominale u0. En réalité, à cause du
bruit, des mesures
répétées d'une même valeur d'exposition donneront des valeurs différentes de u
u = u0 + ε
où ε est une erreur de mesure aléatoire. Cela signifie que chaque
mesure répétée de u aura une valeur différente de ε, mais aussi que
deux pixels voisins qui sont exposés de la même manière donneront des valeurs
de u différentes.
Si on considère qui le bruit est un bruit blanc (ce qui est
probablement faux mais suffisamment similaire à la réalité pour être utile à
cette explication), alors les valeurs de ε sont couramment proches de
zéro (et donc u est proche de u0), mais ε peut parfois,
plus rarement, être nettement plus grand que zéro et donc la valeur de u est
nettement différente de u0.
La sensibilité d'un capteur numérique
Les valeurs typiques de u sont très petites et il est donc nécessaire de les
amplifier avant de les numériser. Ainsi une valeur v de pixel (typiquement entre
0 pour la valeur la plus sombre et 255 pour la valeur la plus lumineuse) est
obtenue en effectuant
v = Au si Au ≤ vmax
v = vmax si Au > vmax
où A est le facteur d'amplification. Comme la valeur de v ne peut dépasser
vmax, on comprend que si l'amplification A choisie est trop élevé
par rapport à u, l'intervalle de valeurs possibles pour un pixel n'est pas
suffisant pour représenter la valeur correcte de ce pixel, et on arrive à la
saturation.
En faisant varier A, on peut faire varier la « sensibilité » du capteur et
obtenir des valeurs élevées de v (donc un pixel très lumineux) à partir d'une
valeur faible de u (par exemple en photographiant dans une situation de faible
luminosité).
Cependant, comme v contient aussi le bruit ε, ce dernier est amplifié
de la même manière :
v = Au0 + Aε
Ainsi, plus la « sensibilité » du capteur est élevée, c'est à dire plus le
facteur d'amplification A est élevé, plus le bruit est élevé et devient
perceptible pour l'observateur.
Par exemple pour une image d'un objet noir, on s'attend à ce que v soit proche
de zéro pour tous les pixels même pour une grande valeur de A parce que
u0 est justement proche de zéro. Mais il peut arriver que ε
soit bien plus grand que u0, ce qui conduit à ce que la valeur v du
pixel soit essentiellement égale à Aε. Ceci se traduit par des pixels
brillants au milieu de pixels sombres, typiques du bruit des photos prises en
faible lumière avec une sensibilité élevée.
Comparaison de capteurs
Dans des conditions d'éclairage uniforme dans l'espace et le temps d'une
surface s pendant un temps t (le temps de pose d'une photo), on peut définir
les grandeurs suivantes :
où Q est la quantité de
lumière
c'est à dire approximativement le nombre de photons qui arrivent sur la
surface s. En combinant ces trois définitions, on obtient
Q = Hs
c'est à dire que la quantité de lumière qui arrive sur un pixel est
proportionnelle à la surface de ce pixel. Autrement dit, à exposition H égale,
un pixel plus grand reçoit une plus grande quantité de lumière qu'un pixel
plus petit.
En reprenant définition de u0 plus haut, on a
u0 = fHs
et donc, en ignorant pour le moment le bruit ε on a
v = AfHs
Ainsi, pour obtenir la même valeur v avec deux capteurs (capteur 1 et capteur
2) dont les pixels ont respectivement des surfaces s1 et
s2, on a besoin d'un facteur d'amplification A1 sur
le capteur 1 et A2 sur le capteur 2 tels que
A2 = A1s1 / s2
On a vu plus haut que le bruit est amplifié. Cela se traduit par
A2ε = A1εs1 / s2
c'est à dire que le bruit dans l'image obtenue par le second capteur est
s1 / s2 fois plus élevé que le bruit dans l'image
obtenue par le premier capteur.
Qualitativement, cela signifie que pour obtenir deux photos exposées de
manière identiques avec deux appareils différents, l'un muni d'un capteur à
grands pixels et le second muni d'un appareil à petits pixels, celui dont les
pixels sont petits a besoin d'un facteur d'amplification plus élevé et
produit donc une image plus bruitée.
Sensibilité
La sensibilité est
définie par S = H0 / H où H0 est une valeur d'exposition
de référence.
Un photographe s'attend à ce que lorsqu'on prend la même photo avec deux
appareils (dont les capteurs sont équivalents à l'exception de la taille des
pixels, et donc de leur nombre), l'image obtenue est exposée de la même façon
(en supposant que la distance focale, le nombre d'ouverture, le temps de pose
et la sensibilité sont les mêmes). Une conséquence est que les facteurs
d'amplification des deux appareils doivent être différents puisque les tailles
des pixels sont différentes, et que l'image de l'appareil dont les pixels sont
plus petits contiendra donc plus de bruit.
Réciproquement, si on cherche à produire avec les deux appareils des images
contenant une quantité de bruit identique, il faut changer les paramètres
d'exposition de l'appareil produisant le plus de bruit de sorte à
- diminuer la sensibilité S d'un facteur s1 / s2 afin
d'utiliser le même facteur d'amplification dans les deux appareils, et
- augmenter l'exposition H d'un facteur s1 / s2 afin
de compenser la diminution de la sensibilité.
On peut parvenir à ce dernier point en augmentant le temps de pose ou en
augmentant la surface de la pupille du diaphragme d'un facteur
s1 / s2.
Selon le modèle simplifié utilisé ici, à tailles de capteurs égales, un
capteur de plus haute définition (donc comportant un plus grand nombre de
pixels) produira donc des images contenant plus de bruit.
Si on décide de considérer qu'avec une exposition de référence Href
la sensibilité Sref maximale d'un capteur de référence dont les
pixels ont une surface sref représente une quantité de bruit de
référence, on peut considérer qu'à quantité de bruit identique, un capteur de
plus haute définition dont les pixels ont une surface s aura donc une
« sensibilité équivalente » Seq plus faible nécessitant une
exposition Heq. En effet
Sref = H0 / Href et
Heq = sref / sHref, donc
Seq = Srefs/sref
Il faut noter que la sensibilité équivalente, qui dépend de la surface des
pixels, n'a rien à voir avec la focale équivalente qui dépend des dimensions
du capteur et non de celles de ses pixels.