Optique photo 1: l'angle de champ
Catégories : [ Science ]
Le modèle simplifié
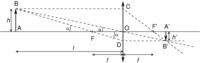
On peut simplifier un objectif d'appareil photo en le considérant comme une lentille mince de centre O et de distance focale f. L'axe optique de la lentille passe par O et est perpendiculaire à cette dernière. Les points F et F', situés de part et d'autre de la lentille à une distance f sont les points focaux de cette dernière. L'objet AB, situé à une distance l de la lentille donne alors une image A'B' sur le capteur de l'appareil photo. La hauteur de l'objet est h et la hauteur de l'image est h'.
Les règles de l'optique géométrique sont simples :
- les rayons lumineux passant par le centre O de la lentille ne sont pas déviés, donc AA' et BB' sont des lignes droites ;
- les rayons lumineux qui arrivent sur la lentille parallèlement à l'axe optique ressortent de la lentille en passant par le point focal F', tel le rayon BCB' ;
- les rayons lumineux qui arrivent sur la lentille en passant par le point focal F ressortent parallèlement à l'axe optique, tel le rayon BDB'.
L'angle de champ
L'angle sous lequel l'objectif voit l'objet AB est l'angle θ. On a tan θ = h / l et tan α = h / (l - f) = h' / f. On en déduit que tan θ = (l - f)h' / lf, que l'on peut simplifier (lorsque f est négligeable devant l) en tan θ = h' / f.
Si on considère que l'image A'B' et son symétrique (qui n'est pas représenté sur le diagramme) sont ensemble suffisamment grands pour couvrir l'intégralité de la diagonale du capteur, on sait que la hauteur h' de l'image représente la moitié de la diagonale d du capteur. Cela signifie que l'angle θ est la moitié de l'angle de champ du système objectif-capteur. On a alors
tan(angle de champ / 2) = d / 2f
Ceci montre que l'angle de champ dépend seulement de la distance focale de l'objectif et de la taille du capteur (lorsque f est négligeable devant l, soit en pratique lorsque la distance à l'objet est au moins dix fois plus grande que la distance focale).
Angle de champ et taille de capteur
Pour deux capteurs de tailles différents et avec un objectif donné, le rapport des tangentes des demi-angles de champ est égale au rapport des tailles des capteurs. Pour des angles de champ de moins de 53° (c.-à-d. lorsque la valeur de la tangente est proche de la valeur de l'angle, en radians), c'est à dire lorsque la distance focale est plus grande que la diagonale du capteur, on peut faire l'approximation que le rapport des angles de champ est égal au rapport des tailles des capteurs, avec une erreur de moins de 10%, soit
angle1 / angle2 = diagonale1 / diagonale2
Ainsi par exemple un capteur deux fois plus grand qu'un autre capteur donnera un angle de champ deux fois plus grand lorsque ces capteurs sont munis d'objectifs de même distance focale.
Si on veut une approximation qui fonctionne aussi pour de grands angles, il devient nécessaire de comparer les tangentes des demi-angles de champ, par exemple
tan(angle1 / 2) / tan(angle2 / 2) = diagonale1 / diagonale2
ou de faire intervenir les arctangentes, par exemple
angle1 / angle2 = arctan(diagonale1 / 2f) / arctan(diagonale2 / 2f)
ce qui est nettement moins pratique à évaluer de tête.
La distance focale équivalente
Supposons que l'on a un capteur de référence dont la diagonale est dref (par exemple un capteur 24×36 mm) et un objectif de distance focale f.
Lorsqu'on utilise cet objectif avec un autre capteur dont la diagonale est d, on a un angle de champ θ défini par
tan(θ / 2) = d / f
On veut alors savoir quelle serait la distance focale équivalente feq d'un objectif fictif donnant le même angle de champ θ si on utilisait cet objectif fictif avec le capteur de référence. On a
tan(θ / 2) = d / f = dref / feq
et donc
feq = f × dref / d
(cette valeur est correcte si f est négligeable par rapport à l et par rapport à ld / dref).
Comparée à l'angle de champ, le calcul de la distance focale équivalente n'est pas limitée à des angles de champ suffisamment petits. La distance focale équivalente fait cependant appel à un facteur caché, la taille du capteur de référence.
[ Posté le 10 septembre 2019 à 22:47 | 3 commentaires | lien permanent ]