Water Rocket Theory
Traduction: [ Google | Babelfish ]
Catégories : [ Bricolage | Science ]
The physics involved in flying a water rocket is not very complex if you have studied a little bit of mechanics and fluid mechanics. It is summarized in a PDF file written by Peter Nielsen, Associate Professor in Civil Engineering of the University of Queensland, Australia. I wrote a Perl script that implements the formulas and outputs data plotable with Gnuplot.
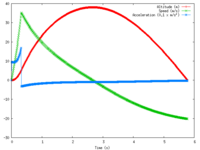
I just finished fixing a bug in the script which was promising wonderful performance of my rocket (like over 200 m altitude and a maximum speed of over 350 km/h), but which were never reached by our rocket. The water rocket that we built last week-end is in theory able to reach 38 m after 2.7 s of flight. Its top speed is 35.5 m/s (126 km/h) after 0.33 s of acceleration, and the acceleration increases from 95 to 169 m/s2 within the same time.
After that, it decelerates during a bit over two seconds, and then starts to drop back to the ground, and lands about 5.8 s after take off (omitting the effect of the parachute).
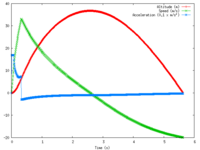
Tuning the parameters of the script, I found the following optimal values: the weight of the rocket should be 140 g, the filling ratio of the water tank should be 0.38 with a pressure of 7 bar, and 0.45 with a pressure of 5 bar. Because of former erroneous calculations, I thought that the optimal filling ratio was about 0.60, which lead to much poorer performance, due to the overload. This second graph shows the theoretical height, speed and acceleration of the rocket during its last flight. The water empties in about 0.32 s, which corresponds to what has been seen on the video clip, and the maximum height is 36.8 m, which seems reasonable (although it has probably never been reached because the parachute opened far too early).
The drag coefficient is one parameter that is very difficult to estimate, and for now its value is 0.9 for the calculations, which is barely better than the one of a brick (about 1.1). Its real value may be less. Or more. Who knows…
Also, the leaks in the pressuring system make it difficult to estimate what was the actual pressure in the rocket at take off. And water was poured without real accuracy, so the above filling ratio may as well be 0.8 or 0.5.
[ Posté le 2 juillet 2007 à 17:06 | pas de commentaire | lien permanent ]